题目内容
求函数f(x)=x2+2xcosθ+1,x∈[-
,
].
(1)当θ=
时,求f(x)的最大值和最小值;
(2)若f(x)在区间[-
,
]上是单调递增函数,θ∈R,求θ的取值范围.
| ||
| 2 |
| 1 |
| 2 |
(1)当θ=
| π |
| 3 |
(2)若f(x)在区间[-
| ||
| 2 |
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:函数的性质及应用
分析:(1)利用三角函数种特殊角的特殊函数值,得到f(x),求出对称轴,然后根据所告诉的区间,求出最值,距离对称轴越远,值越大.
(2)需要分类讨论,当cosθ=0时,不满足条件,当cosθ≠0,再根据对称轴求的cosθ的范围,继而求出θ的范围.
(2)需要分类讨论,当cosθ=0时,不满足条件,当cosθ≠0,再根据对称轴求的cosθ的范围,继而求出θ的范围.
解答:
解:(1)∵θ=
时,则cos
=
∴f(x)=x2+x+1,开口向上,对称轴为x=-
,
∴f(x)在[-
,-
]为减函数,在[-
,
]为增函数,
∴当x=-
,f(x)min=f(-
)=
,
当x=
,f(x)max=f(
)=
,
(2)当cosθ=0时,f(x)=x2+1,在[-
,0)上到单调递减,在[0,
]单调递增,
∵f(x)在区间[-
,
]上是单调递增函数,
∴cosθ=0不成立,
即cosθ≠0,
∵f(x)=x2+2xcosθ+1,x∈[-
,
].
∴对称轴为x=-cosθ,
∴-cosθ≤-
,
即cosθ≥
,
∴2kπ-
≤θ≤2kπ+
,
故θ的取值范围为[2kπ-
,2kπ+
].
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴f(x)=x2+x+1,开口向上,对称轴为x=-
| 1 |
| 2 |
∴f(x)在[-
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
(2)当cosθ=0时,f(x)=x2+1,在[-
| ||
| 2 |
| 1 |
| 2 |
∵f(x)在区间[-
| ||
| 2 |
| 1 |
| 2 |
∴cosθ=0不成立,
即cosθ≠0,
∵f(x)=x2+2xcosθ+1,x∈[-
| ||
| 2 |
| 1 |
| 2 |
∴对称轴为x=-cosθ,
∴-cosθ≤-
| ||
| 2 |
即cosθ≥
| ||
| 2 |
∴2kπ-
| π |
| 6 |
| π |
| 6 |
故θ的取值范围为[2kπ-
| π |
| 6 |
| π |
| 6 |
点评:本题主要考查了二次函数的单调性,关键是求出对称轴,以及观察开口的方向,以及三角函数的取值范围,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
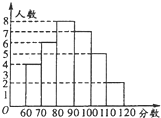 某中学部分学生参加全国高中数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,试题满分120分),并且绘制了“频数分布直方图”,请回答:
某中学部分学生参加全国高中数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,试题满分120分),并且绘制了“频数分布直方图”,请回答: