题目内容
哈尔滨市五一期间决定在省妇女儿中心举行中学生“蓝天绿树、爱护环境”围棋比赛,规定如下:两名选手比赛时每局胜者得1分,负者得0分,比赛进行到有一人比对方多3分或打满7局时停止.设某学校选手甲和选手乙比赛时,甲在每局中获胜的概率为p(p>
),且各局胜负相互独立.已知第三局比赛结束时比赛停止的概率为
.
(1)求p的值;
(2)求甲赢得比赛的概率;
(3)设X表示比赛停止时已比赛的局数,求随机变量X的分布列和数学期望.
| 1 |
| 2 |
| 1 |
| 3 |
(1)求p的值;
(2)求甲赢得比赛的概率;
(3)设X表示比赛停止时已比赛的局数,求随机变量X的分布列和数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由已知得p3+(1-p)3=
,由此能求出p=
.
(2)那么对于甲赢得比赛,需要分为两种情况,连胜三局,或者比赛7局,前6局胜出两局,最后一局甲赢,由此能求出其概率值.
(3)结合题意,X表示比赛停止时已比赛的局数,可知X的可能取值为3,5,7,分别得分为3:0,4:1,5:2,由此能求出随机变量X的分布列和数学期望.
| 1 |
| 3 |
| 2 |
| 3 |
(2)那么对于甲赢得比赛,需要分为两种情况,连胜三局,或者比赛7局,前6局胜出两局,最后一局甲赢,由此能求出其概率值.
(3)结合题意,X表示比赛停止时已比赛的局数,可知X的可能取值为3,5,7,分别得分为3:0,4:1,5:2,由此能求出随机变量X的分布列和数学期望.
解答:
解:(1)根据题意,由于某学校选手甲和选手乙比赛时,
甲在每局中获胜的概率为p(p>
),且各局胜负相互独立.
已知第三局比赛结束时比赛停止的概率为
,
而要是停止的前提是比赛进行到有一人比对方多3分停止,且两名选手比赛时每局胜者得1分,负者得0分,
那么可知p3+(1-p)3=
,解得p=
.
(2)那么对于甲赢得比赛,需要分为两种情况,连胜三局,或者比赛7局,前6局胜出两局,最后一局甲赢,
那么可知其概率值为:p3(1-p)3+
p2(1-p)4p=
.
(3)结合题意,X表示比赛停止时已比赛的局数,
可知X的可能取值为3,5,7,分别得分为3:0,4:1,5:2,
其概率值为P(X=3)=
,P(X=5)=
,P(X=7)=
,
X的分布列为:
期望EX=3×
+5×
+7×
=
.
甲在每局中获胜的概率为p(p>
| 1 |
| 2 |
已知第三局比赛结束时比赛停止的概率为
| 1 |
| 3 |
而要是停止的前提是比赛进行到有一人比对方多3分停止,且两名选手比赛时每局胜者得1分,负者得0分,
那么可知p3+(1-p)3=
| 1 |
| 3 |
| 2 |
| 3 |
(2)那么对于甲赢得比赛,需要分为两种情况,连胜三局,或者比赛7局,前6局胜出两局,最后一局甲赢,
那么可知其概率值为:p3(1-p)3+
| C | 2 6 |
| 152 |
| 243 |
(3)结合题意,X表示比赛停止时已比赛的局数,
可知X的可能取值为3,5,7,分别得分为3:0,4:1,5:2,
其概率值为P(X=3)=
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
X的分布列为:
| X | 3 | 5 | 7 | ||||||
| P |
|
|
|
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 47 |
| 9 |
点评:本题主要是考查了分布列的运用,以及古典概型的概率的运用,属于中档题.

练习册系列答案
相关题目
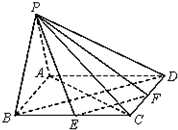 如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PB=PD,且EF分别是BC,CD的中点.求证:
如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PB=PD,且EF分别是BC,CD的中点.求证: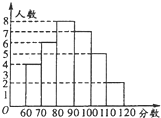 某中学部分学生参加全国高中数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,试题满分120分),并且绘制了“频数分布直方图”,请回答:
某中学部分学生参加全国高中数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,试题满分120分),并且绘制了“频数分布直方图”,请回答: