题目内容
复数z=m2-1+（m+1）i表示纯虚数，则实数m值为（ ）
| A、±1 | B、0 | C、1 | D、-1 |
考点：复数的基本概念
专题：数系的扩充和复数
分析：直接由复数z的实部等于0且虚部不等于0求得m的值．
解答：
解：∵z=m2-1+（m+1）i表示纯虚数，
则
，解得：m=1．
故选：C．
则
|
故选：C．
点评：本题考查了复数的基本概念，考查了复数是纯虚数的条件，是基础题．
练习册系列答案
相关题目
某空间几何体的三视图如图所示，则该几何体的表面积是（ ）
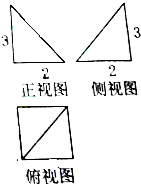
A、10+2
| ||||
B、10+2
| ||||
C、10+
| ||||
D、4+4
|
函数f（x）=sin（2x+
）的最小正周期为（ ）
| π |
| 3 |
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
设i为虚数单位，则复数z=1-i的模|z|=（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
已知全集U=R，若集合A={x|x2-x＜0}，则∁UA=（ ）
| A、{x|x≤0，或x≥1} |
| B、{x|x＜0，或x＞1} |
| C、{x|0＜x＜1} |
| D、{x|x≥1} |
若函数f（x）=ax4+bx2+c满足f′（1）=2，则f′（-1）=（ ）
| A、-1 | B、-2 | C、2 | D、0 |
已知函数f（x）=-x2-2x，g（x）=
若方程g[f（x）]-a=0的实数根的个数有4个，则a的取值范围（ ）
|
A、[1，
| ||
| B、[1，+∞） | ||
| C、（1，+∞） | ||
D、(-
|