题目内容
已知函数f(x)=lg(x-x2),则函数y=f(x2-1)的定义域为 .
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:先由函数的解析式求出函数f(x)的定义域,然后使x-x2在f(x)的定义域中求出x的范围,则函数y=f(x2-1)的定义域可求.
解答:
解:函数y=lg(x-x2)的定义域可由:x-x2>0,解得0<x<1,
又0<x2-1<1,可得-
<x<-1或1<x<
.
函数的定义域为:x∈(-
,-1)∪(1,
).
故答案为:(-
,-1)∪(1,
).
又0<x2-1<1,可得-
| 2 |
| 2 |
函数的定义域为:x∈(-
| 2 |
| 2 |
故答案为:(-
| 2 |
| 2 |
点评:本题考查了函数定义域的求法,训练了复合函数的定义域的求法,求解复合函数的定义域,即如果函数f(x)的定义域为[a,b],则函数f[g(x)]的定义域是满足a≤g(x)≤b的x的取值集合.

练习册系列答案
相关题目
已知x,y都是正数,且xy=1,则x+y的最小值为( )
| A、4 | B、3 | C、2 | D、1 |
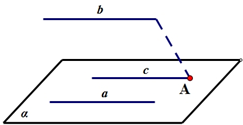 已知直线a在平面α上,直线b不在平面α上,且a∥b,求证:b∥α.
已知直线a在平面α上,直线b不在平面α上,且a∥b,求证:b∥α.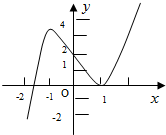 如图,是定义域为R的函数f(x)的图象,f′(x)是函数f(x)的导函数,则不等式xf′(x)>0的解集为
如图,是定义域为R的函数f(x)的图象,f′(x)是函数f(x)的导函数,则不等式xf′(x)>0的解集为