题目内容
若0<a<1,0<b<1,则四个数a+b,2
,2ab,a2+b2中最大者与最小者分别为 .
| ab |
考点:基本不等式
专题:不等式的解法及应用
分析:由0<a<1,0<b<1,可得a>a2,b>b2,0<ab<1.即可得出a+b>a2+b2≥2ab,a+b≥2
>2ab.
| ab |
解答:
解:∵0<a<1,0<b<1,
∴a>a2,b>b2,0<ab<1.
∴a+b>a2+b2≥2ab,
a+b≥2
>2ab.
综上可得:四个数a+b,2
,2ab,a2+b2中最大者与最小者分别为a+b,2ab.
故答案为:a+b,2ab.
∴a>a2,b>b2,0<ab<1.
∴a+b>a2+b2≥2ab,
a+b≥2
| ab |
综上可得:四个数a+b,2
| ab |
故答案为:a+b,2ab.
点评:本题考查了不等式的基本性质和基本不等式的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知复数z1=a-i,z2=1-2i,若
是纯虚数,则实数a的值为( )
| z1 |
| z2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
 如图是正方体的平面展开图,则在这个正方体中,正确的是
如图是正方体的平面展开图,则在这个正方体中,正确的是 如图,在一个边长为2的正方形OABC内,曲线y=-x2+2x与x轴围成如图所示的阴影部分,向正方形OABC内随机投一点(该点落在正方形OABC内的任意一点是等可能的),则点落在阴影部分内的概率为
如图,在一个边长为2的正方形OABC内,曲线y=-x2+2x与x轴围成如图所示的阴影部分,向正方形OABC内随机投一点(该点落在正方形OABC内的任意一点是等可能的),则点落在阴影部分内的概率为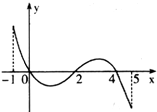 已知函数f(x)的定义域为[-1,5],部分对应值如图:
已知函数f(x)的定义域为[-1,5],部分对应值如图: