题目内容
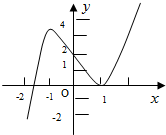如图，是定义域为R的函数f（x）的图象，f′（x）是函数f（x）的导函数，则不等式xf′（x）＞0的解集为考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：由函数y=f（x）（x∈R）的图象可得函数的单调性，根据单调性与导数的关系得导数的符号，进而得不等式xf′（x）＜0的解集．
解答：
解：由图象得：
①-1＜x＜0时，f（x）是减函数，f′（x）＜0，
∴在（-1，0）上，xf′（x）＞0；
②x＞1时，f（x）是增函数，f′（x）＞0，
∴在（1，+∞）上，xf′（x）＞0；
故答案为：（1，+∞）∪（-1，0）．
①-1＜x＜0时，f（x）是减函数，f′（x）＜0，
∴在（-1，0）上，xf′（x）＞0；
②x＞1时，f（x）是增函数，f′（x）＞0，
∴在（1，+∞）上，xf′（x）＞0；
故答案为：（1，+∞）∪（-1，0）．
点评：本题考查导数与函数单调性的关系，考查学生的识图能力，利用导数求函数的单调性是重点．
练习册系列答案
相关题目
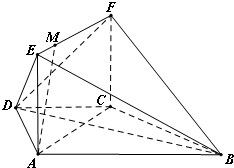如图，在梯形ABCD中，AD⊥CD，AB∥CD，AD=CD=