题目内容
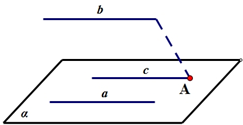 已知直线a在平面α上,直线b不在平面α上,且a∥b,求证:b∥α.
已知直线a在平面α上,直线b不在平面α上,且a∥b,求证:b∥α.(注意:在下面横线上填写适当内容,使之成为完整的证明)
证明:因为直线不在平面α上,所以
下面b∩α=A不可能.
假设b∩α=A,
因为
在平面α上过作直线c∥a,
根据
这和b∩c=A矛盾,所以b∩α=A不可能.
所以b∥α.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:由用反证法证明线面平行的判定定理的过程,逐一补充证明过程中的各空,可得答案.
解答:
用反证法证明线面平行的判定定理的过程如下:
证明:因为直线b不在平面α上,所以b∥α或b∩α=A,
下面b∩α=A不可能.
假设b∩α=A,
因为a∥b,所以A∉a.
在平面α上过作直线c∥a,
根据平行公理,可得b∥c,
这和b∩c=A矛盾,
所以b∩α=A不可能.
所以b∥α.
故答案为:b∥α,a∥b,平行公理,b∥c
证明:因为直线b不在平面α上,所以b∥α或b∩α=A,
下面b∩α=A不可能.
假设b∩α=A,
因为a∥b,所以A∉a.
在平面α上过作直线c∥a,
根据平行公理,可得b∥c,
这和b∩c=A矛盾,
所以b∩α=A不可能.
所以b∥α.
故答案为:b∥α,a∥b,平行公理,b∥c
点评:本题考查的知识点是线面平行的判定定理的证明,熟练掌握反证法证明线面平行的判定定理的过程,是解答的关键.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.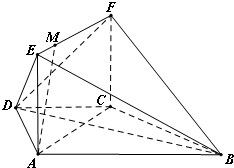 如图,在梯形ABCD中,AD⊥CD,AB∥CD,AD=CD=
如图,在梯形ABCD中,AD⊥CD,AB∥CD,AD=CD=