题目内容
(3x-
)n的展开式中各项系数之和为A,所有偶数项的二项式系数为B,若A+B=96,则展开式中的含有x2的项的系数为( )
| 1 | |||
|
| A、-540 | B、-180 |
| C、540 | D、180 |
考点:二项式系数的性质
专题:二项式定理
分析:求出A和B,再根据A+B=96求得n的值,可得二项式展开式的通项公式,再令x的幂指数等于2,求得r的值,即可求得展开式中的含有x2的项的系数.
解答:
解:令x=1,可得(3x-
)n的展开式中各项系数之和为A=2n,所有偶数项的二项式系数为B=2n-1,
根据A+B=2n+2n-1=3×2n-1=96,∴2n-1=32,∴n=6.
∴(3x-
)n=(3x-
)6的展开式的通项公式为 Tr+1=
•36-r•(-1)r•x6-
,
令6-
=2,求得 r=3,故展开式中的含有x2的项的系数为
•33(-1)=-540,
故选:A.
| 1 | |||
|
根据A+B=2n+2n-1=3×2n-1=96,∴2n-1=32,∴n=6.
∴(3x-
| 1 | |||
|
| 1 | |||
|
| C | r 6 |
| 4r |
| 3 |
令6-
| 4r |
| 3 |
| C | 3 6 |
故选:A.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知函数f(x)(x∈R)满足f(2)=9,且f(x)的导函数f′(x)<
,则f(x)<x3+
x的解集为( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、{x|-2<x<2} |
| B、{x|x<-2} |
| C、{x|x<-2或x>2} |
| D、{x|x>2} |
已知函数y=
,则直线y=x+1与函数图象交点的个数是( )
| 1+x|x| |
| A、0 | B、1 | C、2 | D、3 |
复数
(i为虚数单位)的模为( )
| 2+i |
| i |
A、
| ||
| B、±(1-2i) | ||
C、
| ||
| D、1-2i |
已知集合A={x|x<-1或x≥3},则∁RA等于( )
| A、{x|x<3} |
| B、{x|x>-1} |
| C、{x|-1≤x<3} |
| D、∅ |
A是半径为R的圆周上固定的一点,在该圆周上任取异于A的一点B,则线段AB的长度小于或等于R的概率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在等差数列{an}中,d=
,S100=145,则a1+a3+a5+…+a99的值为( )
| 1 |
| 2 |
| A、57 | B、58 | C、59 | D、60 |
某几何体的三视图如图所示,则该几何体的表面积为( )
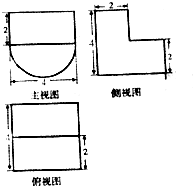

| A、40+12π |
| B、16+8π |
| C、16+16π |
| D、16+32π |