Question

4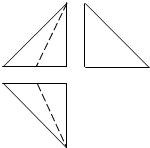．如图是一个四面体的三视图，这个三视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为（　　）

• A． $\frac{2}{3}$
• B． $\frac{4}{3}$
• C． $\frac{8}{3}$
• D． 2

Answer 1

分析 由四面体的三视图得该四面体为棱长为2的正方体ABCD-A₁B₁C₁D₁中的三棱锥C₁-BDE，其中E是CD中点，由此能求出该四面体的体积．

解答 解：由四面体的三视图得该四面体为棱长为2的正方体ABCD-A₁B₁C₁D₁中的三棱锥C₁-BDE，
其中E是CD中点，
△BDE面积$S=\frac{1}{2}×（\frac{1}{2}×2×2）=1$，三棱锥C₁-BDE的高h=CC₁=2，
∴该四面体的体积：
V=$\frac{1}{3}Sh$=$\frac{2}{3}$．
故选：A．

点评 本题考查四面体的体积的求法，是基础题，解题时要认真审题，注意三视图的性质的合理运用．