题目内容
已知(x-1)2+y2=1,点A(-2,0)及点B(3,a),从点A观察点B,要使视线不被圆挡住,则a的取值范围 .
考点:直线与圆的位置关系
专题:直线与圆
分析:设点H(3,0),根据题意画出图形,当直线AB与圆E相切时,此时B与C(或D)重合,求得sin∠HAC=
的值,可得cos∠HAC的值,从而求得tan∠HAC的值.再根据 tan∠HAC=
,求得HC的值,从而求得a的取值范围.
| EF |
| AE |
| HC |
| AH |
解答:
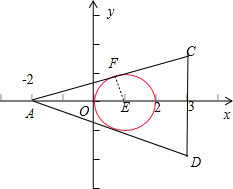 解:设点H(3,0),根据题意画出图形,当AB直线与圆E相切时,B与C(或D)重合),
解:设点H(3,0),根据题意画出图形,当AB直线与圆E相切时,B与C(或D)重合),
此时,sin∠HAC=
=
,∴cos∠HAC=
,∴tan∠HAC=
.
再根据 tan∠HAC=
=
=
,∴HC=
,此时,|a|=
.
要使视线不被圆挡住,则a的取值范围为(-∞,-
)∪(
,+∞),
故答案为:(-∞,-
)∪(
,+∞).
 解:设点H(3,0),根据题意画出图形,当AB直线与圆E相切时,B与C(或D)重合),
解:设点H(3,0),根据题意画出图形,当AB直线与圆E相切时,B与C(或D)重合),此时,sin∠HAC=
| EF |
| AE |
| 1 |
| 3 |
2
| ||
| 3 |
| ||
| 4 |
再根据 tan∠HAC=
| HC |
| AH |
| HC |
| 5 |
| ||
| 4 |
5
| ||
| 4 |
5
| ||
| 4 |
要使视线不被圆挡住,则a的取值范围为(-∞,-
5
| ||
| 4 |
5
| ||
| 4 |
故答案为:(-∞,-
5
| ||
| 4 |
5
| ||
| 4 |
点评:本题主要考查与圆相切的性质,直角三角形中的边角关系、同角三角函数的基本关系,当直线与圆相切时,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
如图,若N=5时,则输出的数等于( )


A、
| ||
B、
| ||
C、
| ||
D、
|
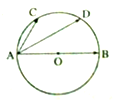
如图,已知AB是圆O的直径,点C,D等分
,已知
=
,
=
,则
等于( )
 |
| AB |
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
执行如图所示的程序框图,则输出的a=( )


A、
| ||
B、-
| ||
| C、5 | ||
D、
|
