题目内容
若函数f(x)=
-
+x+1在区间(
,3)上有极值点,则实数a的取值范围为 .
| x3 |
| 3 |
| ax2 |
| 2 |
| 1 |
| 2 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:求导函数,有极值等价于方程有实根,利用分类讨论的思想,讨论x2-ax+1=0在区间(
,3)上的根的情况,即可求实数a的取值范围.
| 1 |
| 2 |
解答:
解:方法一:f(x)的定义域为R,且 f′(x)=x2-ax+1.
∵f(x)=
-
+x+1在区间(
,3)上有极值点,
∴f′(x)=x2-ax+1=0在区间(
,3)上根,
当 x2-ax+1=0在区间(
,3)有两个实数根时,
∴
即
解得a∈[2,
),
当 x2-ax+1=0在区间(
,3)有一个实数根时,
∴
即
,解得a∈(
,
)
当a=
时,x2-
x+1=0,解得x=
,x=2,其中2∈(
,3)
综上所述,实数a的取值范围为[2,
)
方法二:
由方法一可知,
f′(x)=x2-ax+1=0在区间(
,3)上有根,
∴ax=x2+1,
即a=x+
,等价于求x+
在(
,3)的值域,
即a=x+
≥2
=2,当且仅当x=1取等号,
此时a的最小值为2,
∴
+2=
,3+
=
,
∴a∈[2,
).
故答案为:[2,
).
∵f(x)=
| x3 |
| 3 |
| ax2 |
| 2 |
| 1 |
| 2 |
∴f′(x)=x2-ax+1=0在区间(
| 1 |
| 2 |
当 x2-ax+1=0在区间(
| 1 |
| 2 |
∴
|
|
| 5 |
| 2 |
当 x2-ax+1=0在区间(
| 1 |
| 2 |
∴
|
|
| 5 |
| 2 |
| 10 |
| 3 |
当a=
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,实数a的取值范围为[2,
| 10 |
| 3 |
方法二:
由方法一可知,
f′(x)=x2-ax+1=0在区间(
| 1 |
| 2 |
∴ax=x2+1,
即a=x+
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
即a=x+
| 1 |
| x |
x•
|
此时a的最小值为2,
∴
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 3 |
| 10 |
| 3 |
∴a∈[2,
| 10 |
| 3 |
故答案为:[2,
| 10 |
| 3 |
点评:本题主要考查考查函数的极值和方程根的关系,考查学生的分类讨论的能力,属于中档题.

练习册系列答案
相关题目
如图,已知AB是圆O的直径,点C,D等分
,已知
=
,
=
,则
等于( )
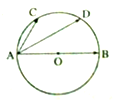
 |
| AB |
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知点P是双曲线
-
=1上一点,M,N是双曲线的左,右顶点,若直线PM的斜率的取值范围是[2,3],则直线PN的斜率的取值范围是( )
| x2 |
| 4 |
| y2 |
| 12 |
A、[1,
| ||||
B、[
| ||||
C、[
| ||||
D、[2,
|
