题目内容
1.已知集合A={1,a,b},B={a,a2,ab},若A=B,求a+b的值.分析 根据集合元素的互异性得到关于a的方程组$\left\{\begin{array}{l}{1={a}^{2}}\\{b=ab}\end{array}\right.$或$\left\{\begin{array}{l}{1=ab}\\{b={a}^{2}}\end{array}\right.$,通过解方程组求得a、b的值,则易求a+b的值.
解答 解:由题意得①组$\left\{\begin{array}{l}{1={a}^{2}}\\{b=ab}\end{array}\right.$或②$\left\{\begin{array}{l}{1=ab}\\{b={a}^{2}}\end{array}\right.$,
由①得a=±1,当a=1时,A={1,1,b},不符合,舍去;
当a=-1时,b=0,A={1,-1,0},B={-1,1,0},符合题意.
由②得a=1,舍去,
所以a+b=-1.
点评 本题考查了集合相等的应用,注意要验证集合中元素的互异性,属于基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
11.下列命题正确的是( )
| A. | 若x≠kπ,k∈Z,则 sin2x+$\frac{2}{si{n}^{2}x}$≥2$\sqrt{2}$ | B. | 若a<0,则a+$\frac{4}{a}$≥-4 | ||
| C. | 若a>0,b>0,则lga+lgb$≥2\sqrt{lga•lgb}$ | D. | 若a<0,b<0,则$\frac{a}{b}+\frac{b}{a}≥2$ |
13.在等差数列{an}中,a1=2,公差为d,则“d=4”是“a1,a2,a5成等比数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.方程$\frac{x^2}{4-t}+\frac{y^2}{t-1}=1$的图象表示曲线C,则以下命题中正确的有( )
①若1<t<4,则曲线C为椭圆;
②若t>4或t<1,则曲线C为双曲线;
③曲线C不可能是圆;
④若曲线C表示椭圆,且长轴在x轴上,则$1<t<\frac{5}{2}$.
①若1<t<4,则曲线C为椭圆;
②若t>4或t<1,则曲线C为双曲线;
③曲线C不可能是圆;
④若曲线C表示椭圆,且长轴在x轴上,则$1<t<\frac{5}{2}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.直线l:y=k(x-2)与双曲线C:x2-y2=2的左右两支各有一个交点,则k的取值范围为( )
| A. | k≤-1或k≥1 | B. | -1≤k≤1 | C. | -$\sqrt{2}$<k<$\sqrt{2}$ | D. | -1<k<1 |
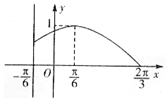 已知定义在区间[-π,$\frac{2}{3}$π]上的函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}<φ<\frac{π}{2}$)的图象关于直线x=-$\frac{π}{6}$对称,当x∈$[-\frac{π}{6},\frac{2π}{3}]$时,f(x)的图象如图所示.
已知定义在区间[-π,$\frac{2}{3}$π]上的函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}<φ<\frac{π}{2}$)的图象关于直线x=-$\frac{π}{6}$对称,当x∈$[-\frac{π}{6},\frac{2π}{3}]$时,f(x)的图象如图所示.