题目内容
6.设函数f(x)=lg(x2-3x)的定义域为集合A,函数$g(x)=\sqrt{-{x^2}+4ax-3{a^2}}$的定义域为集合B(其中a∈R,且a>0).(1)当a=1时,求集合B;
(2)若A∩B≠∅,求实数a的取值范围.
分析 (1)函数$g(x)=\sqrt{-{x^2}+4ax-3{a^2}}$=$\sqrt{-{x}^{2}+4x-3}$,令-x2+4x-3≥0,解出其定义域为集合B=[1,3].
(2)当a>0时,由-x2+4ax-3a2≥0,化为x2-4ax+3a2≤0,解得B=[a,3a].函数f(x)=lg(x2-3x),由x2-3x>0,解得定义域为集合A=(-∞,0)∪(3,+∞),利用A∩B≠∅,即可得出.
解答 解:(1)函数$g(x)=\sqrt{-{x^2}+4ax-3{a^2}}$=$\sqrt{-{x}^{2}+4x-3}$,令-x2+4x-3≥0,化为x2-4x+3≤0,解得1≤x≤3,
其定义域为集合B=[1,3].
(2)当a>0时,由-x2+4ax-3a2≥0,化为x2-4ax+3a2≤0,解得a≤x≤3a.
∴B=[a,3a].
函数f(x)=lg(x2-3x),由x2-3x>0,解得x<0,或x>3,可得定义域为集合A=(-∞,0)∪(3,+∞),
∵A∩B≠∅,所以3a>3,解得a>1.
点评 本题考查了函数的定义域、不等式的解法、集合的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则直线l的斜率为( )
| A. | 1 | B. | -1 | C. | -2或1 | D. | -1或-2 |
15.已知函数f(x)=x2-3x+m+1nx(m∈R)
(1)求f(x)的单调增区间与减区间;
(2)填表(不要求过程,只填结果即可)
(1)求f(x)的单调增区间与减区间;
(2)填表(不要求过程,只填结果即可)
| m的范围 | |||
| 方程f(x)=0的解得个数 | 1 | 2 | 3 |
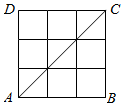 如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.
如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.