题目内容
17.(1)写出命题“若x2-3x+2=0,则x=1或x=2”的逆命题、否命题及逆否命题;(2)写出命题“?x0∈R,使得x02+x0-1<0”的否定形式.
分析 (1)根据逆命题、否命题,以及逆否命题的定义即可得到结果;
(2)写出命题的否定形式即可.
解答 解:(1)命题“若x2-3x+2=0,则x=1或x=2”的逆命题为:若x=1或x=2,则x2-3x+2=0;
否命题为:若x2-3x+2≠0,则x≠1且x≠2;
逆否命题;若x≠1且x≠2,则x2-3x+2≠0;
(2)命题的否定:?x∈R,使得x2+x-1≥0.
点评 此题考查了四种命题,以及命题的否定,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
7.圆C1:x2+y2-2x-6y+1=0与圆C2:x2+y2+4x+2y+1=0的公切线有且仅有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
8.一个物体的运动方程是s=3tcost+x(x为常数),则其速度方程为( )
| A. | v=3cost-3tsint+1 | B. | v=3cost-3tsint | ||
| C. | v=-3sint | D. | v=3cost+3tsint |
5.已知函数f(x)=$\frac{x}{x+1}$+2x-mln(x+1)在(0,+∞)上是增函数,则实数m的取值范围为( )
| A. | (-∞,2$\sqrt{2}$] | B. | (-∞,2$\sqrt{2}$) | C. | (-∞,3) | D. | (-∞,3] |
2.设函数f(x)=|2x-1|,c<b<a,且f(c)>f(a)>f(b),则下列关系式正确的是( )
| A. | a+c≤0 | B. | a+c>0 | C. | a+c≤0 | D. | a+c<0 |
9.若复数z满足$\frac{z}{(1+i)^{2}}$=cos60°+isin60°,其中i为虚数单位,则z=( )
| A. | -$\sqrt{3}$-i | B. | -$\sqrt{3}$+i | C. | 1+$\sqrt{3}$i | D. | 1-$\sqrt{3}$i |
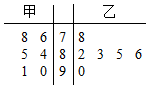 吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示:
吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示: