题目内容
讨论函数f(x)=
ax2+x-(a+1)lnx在a∈R时的单调性.
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:由题意确定函数的定义域,再求导f′(x)=ax+1-(a+1)
=
,分5种情况讨论导数的正负,以确定函数的单调性.
| 1 |
| x |
| (ax+a+1)(x-1) |
| x |
解答:
解:f(x)=
ax2+x-(a+1)lnx的定义域为(0,+∞),
f′(x)=ax+1-(a+1)
=
,
①当a≥0时,ax+a+1>0,
故当x∈(0,1)时,f′(x)<0,当x∈(1,+∞)时,f′(x)>0;
故f(x)在(0,1)上是减函数,在(1,+∞)上是增函数;
f′(x)=
,
②当-
<a<0时,
<-1;
故当x∈(0,1)∪(-
,+∞)时,f′(x)<0,当x∈(1,-
)时,f′(x)>0;
故f(x)在(0,1),(-
,+∞)上是减函数,在(1,-
)上是增函数;
③当-1<a<-
时,-1<
<0;
故当x∈(0,-
)∪(1,+∞)时,f′(x)<0,当x∈(-
,1)时,f′(x)>0;
故f(x)在(0,-
),(1,+∞)上是减函数,在(-
,1)上是增函数;
④当a=-
时,f′(x)≤0;
故f(x)在(0,+∞)上是减函数,
⑤当a≤-1时,ax+a+1<0,
故故当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0;
故f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
| 1 |
| 2 |
f′(x)=ax+1-(a+1)
| 1 |
| x |
=
| (ax+a+1)(x-1) |
| x |
①当a≥0时,ax+a+1>0,
故当x∈(0,1)时,f′(x)<0,当x∈(1,+∞)时,f′(x)>0;
故f(x)在(0,1)上是减函数,在(1,+∞)上是增函数;
f′(x)=
a(x+
| ||
| x |
②当-
| 1 |
| 2 |
| a+1 |
| a |
故当x∈(0,1)∪(-
| a+1 |
| a |
| a+1 |
| a |
故f(x)在(0,1),(-
| a+1 |
| a |
| a+1 |
| a |
③当-1<a<-
| 1 |
| 2 |
| a+1 |
| a |
故当x∈(0,-
| a+1 |
| a |
| a+1 |
| a |
故f(x)在(0,-
| a+1 |
| a |
| a+1 |
| a |
④当a=-
| 1 |
| 2 |
故f(x)在(0,+∞)上是减函数,
⑤当a≤-1时,ax+a+1<0,
故故当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0;
故f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
点评:本题考查了导数的综合应用及分类讨论的思想,分类标准比较难,属于难题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
已知a,b,c是正实数,则“
b=a+2c”是“b2≥4ac”的( )
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
一个几何体的三视图如图所示,则该几何体的体积是( )


| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
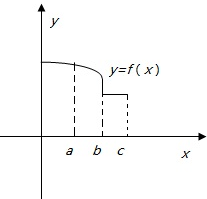 函数y=f(x)的图象如图所示,试画出导函数f′(x)的大致形状.
函数y=f(x)的图象如图所示,试画出导函数f′(x)的大致形状.