题目内容
已知函数f（x）=lnx，当x＞0时，f（x）＜ax恒成立，求a的取值范围．
考点：函数恒成立问题
专题：计算题,函数的性质及应用,导数的综合应用
分析：当x＞0时，f（x）＜ax恒成立，即为a＞
恒成立，令g（x）=
，求出导数，得到极大值也为最大值，令a大于最大值即可．
| lnx |
| x |
| lnx |
| x |
解答：
解：当x＞0时，f（x）＜ax恒成立，
即为a＞
恒成立，
令g（x）=
，g′（x）=
，
当x＞e，时，g′（x）＜0，g（x）递减，
当0＜x＜e，时，g′（x）＞0，g（x）递增．
则x=e为g（x）的极大值点，也为最大值点，
且g（x）最大值为
．
则a＞
．
即为a＞
| lnx |
| x |
令g（x）=
| lnx |
| x |
| 1-lnx |
| x2 |
当x＞e，时，g′（x）＜0，g（x）递减，
当0＜x＜e，时，g′（x）＞0，g（x）递增．
则x=e为g（x）的极大值点，也为最大值点，
且g（x）最大值为
| 1 |
| e |
则a＞
| 1 |
| e |
点评：本题考查函数的恒成立问题，注意转化为求函数的最值，考查导数的运用，考查运算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知sin(x-
)cos(x-
)=-
，则cos4x的值等于（ ）
| 3π |
| 4 |
| π |
| 4 |
| 1 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果一个数列{an}满足an+1+an=h（h为常数，n∈N*），则称数列{an}为等和数列，h为公和，Sn是其前n项的和，已知等和数列{an}中，a1=1，h=-3，则S2015等（ ）
| A、3020 | B、3021 |
| C、-3020 | D、-3021 |
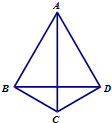如图，将两个全等的30°的直角三角形ABC和直角三角形ADC拼在一起组成平面四边形ABCD，若| DB |
| DA |
| DC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知f（x6）=log2x，则f（8）=（ ）
A、
| ||
| B、8 | ||
| C、18 | ||
D、
|