题目内容
已知函数f(x)=
cos(2x-
)+2sin2(x-
),钝角△ABC(角A、B、C所对的边长分别为 a、b、c)的角B满足f(B)=1.
(1)求函数f(x)的单调递增区间;
(2)若b=3,c=3
,求B、a.
| 3 |
| 2π |
| 3 |
| π |
| 12 |
(1)求函数f(x)的单调递增区间;
(2)若b=3,c=3
| 3 |
考点:三角函数中的恒等变换应用,正弦定理,余弦定理
专题:常规题型,三角函数的图像与性质,解三角形
分析:第(1)问利用三角恒等变换化成y=Asin(ωx+φ)的形式,然后再研究函数的单调性;第(2)问根据条件f(B)=1求出角B,然后利用余弦定理解出a.
解答:
解:(1)f(x)=
cos(2x-
)+2sin2(x-
)
=-
+
sin2x+1-cos(2x-
)
=2sin(2x-
)+1
由2kπ-
≤2x-
≤2kπ+
得kπ-
≤x≤kπ+
(k∈Z)
所以函数f(x)的单调递增区间为[kπ-
,kπ+
](k∈Z)
(2)由f(B)=1得sin(2B-
)=0,解得2B-
=kπ(k∈Z)
又因为b<c,所以B=
,
由余定理得:32=(3
)2+a2-6
acos
解得a=3或a=6
又因为△ABC是钝角三角形,所以a=3.
| 3 |
| 2π |
| 3 |
| π |
| 12 |
=-
| ||
| 2 |
| ||
| 2 |
| π |
| 6 |
=2sin(2x-
| π |
| 3 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
所以函数f(x)的单调递增区间为[kπ-
| π |
| 12 |
| 5π |
| 12 |
(2)由f(B)=1得sin(2B-
| π |
| 3 |
| π |
| 3 |
又因为b<c,所以B=
| π |
| 6 |
由余定理得:32=(3
| 3 |
| 3 |
| π |
| 6 |
解得a=3或a=6
又因为△ABC是钝角三角形,所以a=3.
点评:本题考查了求三角函数的单调区间,关键是通过三角恒等变换化成标准形式;第(2)问考查了利用正、余弦定理解三角形.

练习册系列答案
相关题目
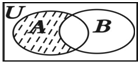 已知全集U为实数集R,集合A={x|0<x<2},集合B={x|lgx>0},则图中阴影部分表示的集合为( )
已知全集U为实数集R,集合A={x|0<x<2},集合B={x|lgx>0},则图中阴影部分表示的集合为( )| A、{0|0<x≤1} |
| B、{x|0<x<2} |
| C、{x|x<1} |
| D、∅ |
在△ABC中,若a=2,b+c=7,cosB=-
,则b=( )
| 1 |
| 4 |
| A、3 | B、4 | C、5 | D、6 |
 如图所示,一条直角走廊宽为a米.现有一转动灵活的平板车,其平板面为矩形,它的宽为b(0<b<a)米.
如图所示,一条直角走廊宽为a米.现有一转动灵活的平板车,其平板面为矩形,它的宽为b(0<b<a)米.