题目内容
如图所示，一条直角走廊宽为a米．现有一转动灵活的平板车，其平板面为矩形，它的宽为b（0＜b＜a）米．（1）若平板车卡在直角走廊内，且∠CAB=θ，试求平板面的长l．
（2）若平板车要想顺利通过直角走廊，其长度不能超过多少米？
考点：已知三角函数模型的应用问题
专题：综合题,三角函数的求值
分析：（1）设矩形为ABEF，直线EF分别交直线AC，BC于M，N，过点D作DP⊥AC于P，过点D作DQ⊥BC于Q，求出DM，DN，MF，EN，即可求平板面的长l．
（2）换元，确定函数的单调性，即可得出结论．
（2）换元，确定函数的单调性，即可得出结论．
解答：
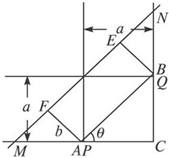解：（1）如图，设矩形为ABEF，直线EF分别交直线AC，BC于M，N，过点D作DP⊥AC于P，过点D作DQ⊥BC于Q，则DM=
，DN=
MF=
，EN=btanθ
所以l=DM+DN-MF-EN=
+
-btanθ-
=
（2）设t=sinθ+cosθ=
sin(θ+
)∈(1，
]，
则l=
=
+
因为函数y=
和y=
在区间(1，
]上均为减函数
所以l=
=
+
在(1，
]上单调递减
所以lmin=
+2a-2b=2
a-2b
故平板车的长度不能超过2
a-2b米
解：（1）如图，设矩形为ABEF，直线EF分别交直线AC，BC于M，N，过点D作DP⊥AC于P，过点D作DQ⊥BC于Q，则DM=| a |
| sinθ |
| a |
| cosθ |
| b |
| tanθ |
所以l=DM+DN-MF-EN=
| a |
| sinθ |
| a |
| cosθ |
| b |
| tanθ |
| a(sinθ+cosθ)-b |
| sinθcosθ |
（2）设t=sinθ+cosθ=
| 2 |
| π |
| 4 |
| 2 |
则l=
| 2at-2b |
| t2-1 |
| 2a |
| t+1 |
| 2a-2b |
| t2-1 |
因为函数y=
| 2a |
| t+1 |
| 2a-2b |
| t2-1 |
| 2 |
所以l=
| 2at-2b |
| t2-1 |
| 2a |
| t+1 |
| 2a-2b |
| t2-1 |
| 2 |
所以lmin=
| 2a | ||
|
| 2 |
故平板车的长度不能超过2
| 2 |
点评：本题考查利用数学知识解决实际问题，考查三角函数知识的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知复数z=
的虚部为0，则实数m的值为（ ）
| m+2i |
| 3-4i |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
某校内有一块以O为圆心，R（R为常数，单位为米）为半径的半圆形（如图）荒地，该校总务处计划对其开发利用，其中弓形BCDB区域（阴影部分）用于种植学校观赏植物，△OBD区域用于种植花卉出售，其余区域用于种植草皮出售．已知种植学校观赏植物的成本是每平方米20元，种植花卉的利润是每平方米80元，种植草皮的利润是每平方米30元．