题目内容
【题目】某公园为了美化环境和方便顾客,计划建造一座圆弧形拱桥,已知该桥的剖面如图所示,共包括圆弧形桥面![]() 和两条长度相等的直线型路面
和两条长度相等的直线型路面![]() 、
、![]() ,桥面跨度
,桥面跨度![]() 的长不超过
的长不超过![]() 米,拱桥
米,拱桥![]() 所在圆的半径为
所在圆的半径为![]() 米,圆心
米,圆心![]() 在水面
在水面![]() 上,且
上,且![]() 和
和![]() 所在直线与圆
所在直线与圆![]() 分别在连结点
分别在连结点![]() 和
和![]() 处相切.设
处相切.设![]() ,已知直线型桥面每米修建费用是
,已知直线型桥面每米修建费用是![]() 元,弧形桥面每米修建费用是
元,弧形桥面每米修建费用是![]() 元.
元.
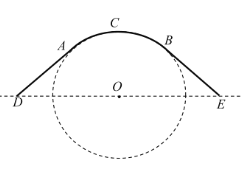
(1)若桥面(线段![]() 、
、![]() 和弧
和弧![]() )的修建总费用为
)的修建总费用为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,桥面修建总费用
为何值时,桥面修建总费用![]() 最低?
最低?
【答案】(1)![]() ,
,![]() .(2)
.(2)![]()
【解析】
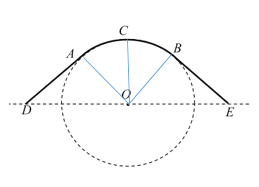
(1)设![]() 为弧
为弧![]() 的中点,连结
的中点,连结![]() ,
,![]() ,
,![]() ,通过解直角三角形以及弧长公式,求得
,通过解直角三角形以及弧长公式,求得![]() 的长,由此计算出修建总费用
的长,由此计算出修建总费用![]() 的表达式,根据
的表达式,根据![]() 长度的限制,和圆的直径,求得
长度的限制,和圆的直径,求得![]() 的取值范围.
的取值范围.
(2)利用导数求得![]() 的单调区间,进而求得当
的单调区间,进而求得当![]() 为何值时,
为何值时,![]() 取得最小值.
取得最小值.
(1)设![]() 为弧
为弧![]() 的中点,连结
的中点,连结![]() ,
,![]() ,
,![]() ,则
,则![]()
在![]() 中,
中,![]() .
.
又因为![]() ,所以弧
,所以弧![]() 长为
长为![]() ,
,
所以![]()
![]()
![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]()
所以![]() ,
,![]() .
.
(2)设![]() ,则
,则![]() ,令
,令![]() 得
得![]()
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
所以当![]() 时,函数
时,函数![]() 取得最小值,此时桥面修建总费用最低.
取得最小值,此时桥面修建总费用最低.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目