题目内容
【题目】已知函数![]() (
(![]() ,
,![]() 是实数常数)的图像上的一个最高点是
是实数常数)的图像上的一个最高点是![]() ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是![]() .
.
(1)求函数![]() 的解析式及其单调递增区间;
的解析式及其单调递增区间;
(2)在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() ,角
,角![]() 的取值范围是区间
的取值范围是区间![]() 。当
。当![]() 时,试求函数
时,试求函数![]() 的取值范围。
的取值范围。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先根据配角公式化简函数解析式,再根据条件得周期解得![]() ,代入最高点坐标解得c,最后根据正弦函数性质求增区间,(2)先根据向量数量积解得角B,再根据三角形内角关系求角
,代入最高点坐标解得c,最后根据正弦函数性质求增区间,(2)先根据向量数量积解得角B,再根据三角形内角关系求角![]() 的取值范围,最后根据正弦函数性质求函数值域.
的取值范围,最后根据正弦函数性质求函数值域.
(1)∵![]() ,∴
,∴![]() .
.
∵![]() 和
和![]() 分别是函数图像上相邻的最高点和最低点,
分别是函数图像上相邻的最高点和最低点,
∴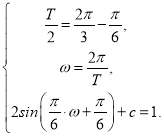 ,解得
,解得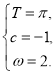 ∴
∴![]() .
.
由![]() ,解得
,解得![]() .
.
∴函数![]() 的单调递增区间是
的单调递增区间是![]() .
.
(2)∵在![]() 中,
中,![]() ,∴
,∴![]() .
.
∴![]() ,即
,即![]() . ∴
. ∴![]() .
.
当![]() 时,
时,![]() ,考察正弦函数
,考察正弦函数![]() 的图像,
的图像,
可知,![]() .∴
.∴![]() ,即函数
,即函数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目