题目内容
【题目】已知函数
，
．
（1）讨论
的单调性；
（2）若有两个极值点
，求
的最大值．
【答案】（1）分类讨论，详见解析；（2）
.
【解析】
（1）求出导函数，根据二次函数的
与
的关系来分类讨论函数的单调性，并注意一元二次方程根的正负与定义域的关系；
（2）由
是两个极值点得到对应的韦达定理形式，然后利用条件将
转变为关于某一变量的新函数，分析新函数的单调性从而确定出新函数的最大值即的最大值.
（1）
，
，
，
当
，即
时，
，此时
在
上单调递增；
当
时，
有两个负根，此时在上单调递增；
当
时，有两个正根，分别为
，
，
此时在
，
上单调递增，在
上单调递减．
综上可得:
时，在上单调递增，
时，在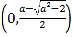
，
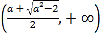上单调递增，在
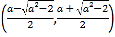上单调递减．
（2）由（1）可得
，，
，
，
∵，
，∴
，
，
∴
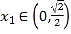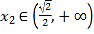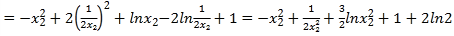
令
，则
当
时，
；当
时，
∴
在
上单调递增，在
单调递减
∴
∴的最大值为．
练习册系列答案
相关题目
