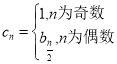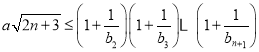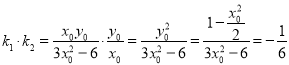题目内容
【题目】已知函数![]() .
.
(1)若对任意的![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)设![]() ,若
,若![]() 为曲线
为曲线![]() 上的两个不同的点,满足
上的两个不同的点,满足![]() ,且
,且![]() ,使得曲线
,使得曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求证:
平行,求证:![]() .
.
【答案】(1)1;(2)证明见解析
【解析】
(1) 对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立aln(x+1)﹣x![]() .
.
令h(x)=aln(x+1)﹣x![]() (x≥0).利用导数的运算法则可得h′(x)
(x≥0).利用导数的运算法则可得h′(x)![]() .
.
分类讨论:当a≥1时,当a<1时,只要验证最小值是否大于0即可得出.
(2)p(x)=f(x﹣1)=alnx,kAB![]() .利用导数的运算法则可得
.利用导数的运算法则可得![]() .由于曲线y=f(x)在x3处的切线与直线AB平行,可得
.由于曲线y=f(x)在x3处的切线与直线AB平行,可得![]() .利用p′(x)在定义域内单调性质要证:x3
.利用p′(x)在定义域内单调性质要证:x3![]() .即证明
.即证明![]() .即证明
.即证明![]() .变形可得
.变形可得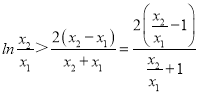 ,令
,令![]() ,则t>1.要证明的不等式等价于
,则t>1.要证明的不等式等价于![]() (t+1)lnt>2(t﹣1).构造函数q(t)=(t+1)lnt﹣2(t﹣1),(t>1).利用导数研究其单调性即可证明.
(t+1)lnt>2(t﹣1).构造函数q(t)=(t+1)lnt﹣2(t﹣1),(t>1).利用导数研究其单调性即可证明.
(1)![]() 恒成立
恒成立![]() 恒成立,
恒成立,
令![]() ,
,
则![]() ,
,
(i)若![]() ,则
,则![]() 恒成立,
恒成立,
![]() 函数
函数![]() 在
在![]() 为单调递增函数,
为单调递增函数,
![]() 恒成立,又
恒成立,又![]() ,
,
![]() 符合条件.
符合条件.
(ii)若![]() ,由
,由![]() ,可得
,可得![]() ,
,
解得![]() 和
和![]() (舍去),
(舍去),
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
∴![]() ,这与h(x)≥0相矛盾,应舍去.
,这与h(x)≥0相矛盾,应舍去.
综上,![]() ,
,![]() 的最小值为1.
的最小值为1.
(2)![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
由![]() ,易知其在定义域内为单调递减函数,
,易知其在定义域内为单调递减函数,
欲证![]() 证明
证明![]() ,
,
即![]() ,
,
变形可得: ,
,
令![]() ,原不等式等价于
,原不等式等价于![]() ,
,
等价于![]() ,
,
构造函数![]() ,
,
则![]() ,
,
令![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,![]() ,
,
![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
![]()
![]() 在
在![]() 上恒成立,
上恒成立,
![]() 成立,
成立,![]() 得证.
得证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目