题目内容
1.在锐角△ABC中,若sinA=3sinBsinC,则tanAtanBtanC的最小值是12.分析 结合三角形关系和式子sinA=2sinBsinC可推出sinBcosC+cosBsinC=3sinBsinC,进而得到tanB+tanC=3tanBtanC,结合函数特性可求得最小值.
解答 解:由sinA=sin(π-A)=sin(B+C)=sinBcosC+cosBsinC,sinA=3sinBsinC,
可得sinBcosC+cosBsinC=3sinBsinC,①
由三角形ABC为锐角三角形,则cosB>0,cosC>0,
在①式两侧同时除以cosBcosC可得tanB+tanC=3tanBtanC,
又tanA=-tan(π-A)=-tan(B+C)=-$\frac{tanB+tanC}{1-tanBtanC}$②,
则tanAtanBtanC=-$\frac{tanB+tanC}{1-tanBtanC}$•tanBtanC,
由tanB+tanC=3tanBtanC,可得tanAtanBtanC=-$\frac{3(tanBtanC)^{2}}{1-tanBtanC}$,
令tanBtanC=t,由A,B,C为锐角可得tanA>0,tanB>0,tanC>0,
由②式得1-tanBtanC<0,解得t>1,
tanAtanBtanC=-$\frac{3{t}^{2}}{1-t}$=-$\frac{3}{\frac{1}{{t}^{2}}-\frac{1}{t}}$,$\frac{1}{{t}^{2}}$-$\frac{1}{t}$=($\frac{1}{t}$-$\frac{1}{2}$)2-$\frac{1}{4}$,由t>1得,-$\frac{1}{4}$≤$\frac{1}{{t}^{2}}$-$\frac{1}{t}$<0,
因此tanAtanBtanC的最小值为12.
故答案为:12.
点评 本题考查了三角恒等式的变化技巧和函数单调性知识,考查了转化思想,有一定灵活性,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案| A. | $\frac{π-2}{2}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
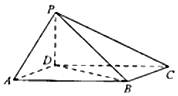 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.