题目内容
用反证法证明命题：设x、y、z∈R+，a=x+
，b=y+
，c=z+
，则a、b、c三个数至少有一个不小于2，下列假设中正确的是（ ）
| 1 |
| y |
| 1 |
| z |
| 1 |
| x |
| A、假设a，b，c三个数至少有一个不大于2 |
| B、假设a，b，c三个数都不小于2 |
| C、假设a，b，c三个数至多有一个不大于2 |
| D、假设a，b，c三个数都小于2 |
考点：反证法与放缩法
专题：不等式的解法及应用
分析：由条件求出要证命题的否定，可得结论．
解答：
解：由于命题：“a、b、c三个数至少有一个不小于2”的否定为：“a，b，c三个数都小于2”，
结合用反证法证明数学命题的方法，
故选：D．
结合用反证法证明数学命题的方法，
故选：D．
点评：本题主要考查用反证法证明数学命题的方法和步骤，求一个命题的否定，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
数列{n2+n}中的项不能是（ ）
| A、380 | B、342 |
| C、321 | D、306 |
在△ABC中，若
•
=3
•
，cosC=
，则A的大小为（ ）
| AB |
| AC |
| BA |
| BC |
| ||
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
（文科）sin
π等于（ ）
| 2009 |
| 4 |
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|
已知M?{1，2，3}，且M?{1，2，4，5}，则满足上述条件的集合M的个数是（ ）
| A、3 | B、4 | C、7 | D、15 |
正六棱锥P-ABCDEF中，G为PB的中点，则三棱锥D-GAC与三棱锥E-GAC的体积比
为（ ）
| VD-GAC |
| VE-GAC |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
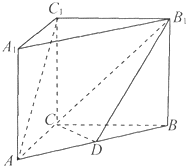如图，在三棱柱ABC-A1B1C1中，C1C⊥底面ABC，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．