题目内容
17.已知i为虚数单位,则复数$Z=\frac{{1-\sqrt{3}i}}{{\sqrt{3}+i}}$的虚部为( )| A. | 1 | B. | -1 | C. | i | D. | -i |
分析 利用复数的运算法则、共轭复数的定义、虚部的定义即可得出.
解答 解:复数$Z=\frac{{1-\sqrt{3}i}}{{\sqrt{3}+i}}$=$\frac{-i(i+\sqrt{3})}{\sqrt{3}+i}$=-i,其虚部为-1.
故选:B.
点评 本题考查了复数的运算法则、共轭复数的定义、虚部的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
8.已知正项等比数列{an}的前n项和为Sn,已知S4-S1=7a2,a3=5,则Sn=( )
| A. | $\frac{5}{2}({2}^{n}-1)$ | B. | $\frac{5}{18}({3}^{n}-1)$ | C. | $5•{2}^{n-1}-\frac{5}{4}$ | D. | $5•{2}^{n-2}-\frac{5}{4}$ |
4.一个几何体的正视图,侧视图为边长为2的正方形,其全面积为( )
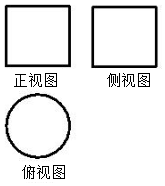

| A. | 6π | B. | $8\sqrt{2}$π | C. | $4+4\sqrt{2}$π | D. | $8+4\sqrt{2}$π |
1.近年来,某地区为促进本地区发展,通过不断整合地区资源、优化投资环境、提供投资政策扶持等措施,吸引外来投资,效果明显.该地区引进外来资金情况如表:
(Ⅰ)求y关于t的回归直线方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$;
(Ⅱ)根据所求回归直线方程预测该地区2017年(t=6)引进外来资金情况.
参考公式:回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$中斜率和截距的最小二乘估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$t.
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 外来资金y(百亿元) | 5 | 6 | 7 | 8 | 10 |
(Ⅱ)根据所求回归直线方程预测该地区2017年(t=6)引进外来资金情况.
参考公式:回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$中斜率和截距的最小二乘估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$t.
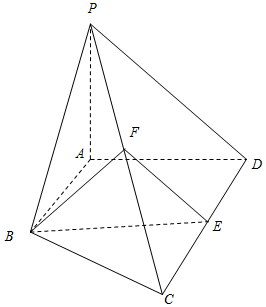 如图,在四棱锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
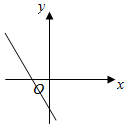
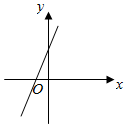

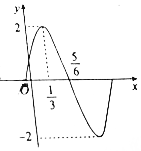 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于函数f(x)的性质的结论正确的有①②③④(填序号)
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于函数f(x)的性质的结论正确的有①②③④(填序号)