题目内容
12.在空间四边形ABCD中,AB⊥CD,BC⊥AD,AC与BD的位置关系是垂直.分析 作BP垂直于平面ADC,P是垂足,连接CP,DP,AP,CP,DP,AP分别是BC,BD,AB在平面ABC内的射影,由BC⊥AD,AB⊥CD,知点P是△ADC的垂心.故DP垂直于AC.由三垂线定理,知BD⊥AC.
解答 解:作BP垂直于平面ADC,P是垂足,连接CP,DP,AP,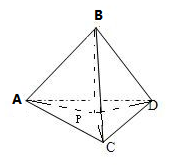
CP,DP,BP分别是BC,BD,AB在平面ACD内的射影,
∵BC⊥AD,
∴由三垂线定理的逆定理知AD⊥CP.
∵AB⊥CD,
∴由三垂线定理的逆定理知CD⊥AP,
∴点P是△ADC的垂心.
∴DP垂直于AC.
由三垂线定理,知BD⊥AC.
故答案为:垂直.
点评 本题考查空间中直线与直线之间的位置关系,是基础题.解题时要认真审题,仔细解答,注意三垂线定理及其逆定理的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.一个正三棱柱的主视图如图所示,则其左视图的面积( )


| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
17.已知tanα<0,则( )
| A. | sinα<0 | B. | sin2α<0 | C. | cosα<0 | D. | cos2α<0 |