题目内容
2.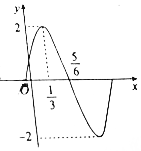 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于函数f(x)的性质的结论正确的有①②③④(填序号)
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于函数f(x)的性质的结论正确的有①②③④(填序号)①f(x)的图象关于点(-$\frac{1}{6}$,0)对称;
②f(x)的图象关于直线x=$\frac{4}{3}$对称;
③f(x)在[-$\frac{1}{2},\frac{1}{3}$]上为增函数;
④把f(x)的图象向右平移$\frac{2}{3}$个单位长度,得到一个偶函数的图象.
分析 由图象可得A=2,$\frac{T}{4}=\frac{π}{2ω}=\frac{5}{6}-\frac{1}{3}$⇒ω=2,故函数的解析式为:f(x)=2sin(πx+ϕ),
代入点($\frac{5}{6},0)$得2$sin(\frac{5π}{6}+ϕ)=0$,解得解得ϕ=$\frac{π}{6}$,
故函数的解析式为:f(x)=2sin(πx+$\frac{π}{6}$),再根据三角函数性质判定答案.
解答 解:由图象可得A=2,$\frac{T}{4}=\frac{π}{2ω}=\frac{5}{6}-\frac{1}{3}$⇒ω=2,
故函数的解析式为:f(x)=2sin(πx+ϕ),
代入点($\frac{5}{6},0)$得2$sin(\frac{5π}{6}+ϕ)=0$,解得解得ϕ=$\frac{π}{6}$,
故函数的解析式为:f(x)=2sin(πx+$\frac{π}{6}$).
对于①,∵f(-$\frac{1}{6}$)=0,∴f(x)的图象关于点(-$\frac{1}{6}$,0)对称,故正确;
对于②,∵f($\frac{4}{3}$)=-2为最小值,∴f(x)的图象关于直线x=$\frac{4}{3}$对称,故正确;
对于③,f(x)=2sin(πx+$\frac{π}{6}$)的增区间为[2k-.$\frac{2}{3},2k+\frac{1}{3}$],∴f(x)在[-$\frac{1}{2},\frac{1}{3}$]上为增函数,故正确;
对于④,把f(x)的图象向右平移$\frac{2}{3}$个单位长度,得到y=2sin(πx-$\frac{π}{2}$)=-2cosπx是一个偶函数,故正确.
故答案为:①②③④
点评 本题考查由图象确定函数f(x)=Asin(ωx+ϕ)的解析式,及三角函数的性质,属中档题.

 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 10 | B. | $10+2\sqrt{3}$ | C. | $10+2\sqrt{5}$ | D. | 12 |
| A. | -ln2 | B. | ln2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |
| A. | -1<a≤0 | B. | -1<a<0 | C. | a>-1 | D. | 0<a≤1 |
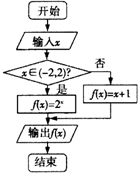
| A. | [0,log23] | B. | [-2,2] | C. | [0,log23]∪{2} | D. | [-2,log23]∪{2} |
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |