题目内容

4．一个几何体的正视图，侧视图为边长为2的正方形，其全面积为（　　）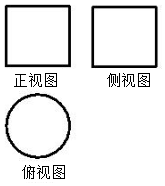
A．6πB．$8\sqrt{2}$πC．$4+4\sqrt{2}$πD．$8+4\sqrt{2}$π

分析 由已知可得该几何体为圆柱，将半径和高代入圆柱表面积公式，可得答案．

解答 解：由三视图可得该几何体为圆柱，
且底面直径为2，半径为r=1，高为h=2，
所以圆柱体的全面积为
S=2πr（r+h）=2π×1×（1+2）=6π．
故选：A．

点评 本题要先根据三视图确定出是什么几何体再根据其表面积公式进行计算，是基础题目．

练习册系列答案
相关题目
19．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点为A，上顶点为B，右焦点为F，设线段AB的中点为M，若2$\overrightarrow{MA}$•$\overrightarrow{MF}$+$\overrightarrow{BF}$2＜0，则该椭圆离心率的取值范围为（$\sqrt{3}$-1，1）．
20．已知函数$f（x）=\frac{1-x}{1+{x}^{2}}{e}^{x}$．
（Ⅰ）求f（x）在点（0，f（0））处的切线方程；
（Ⅱ）证明：当f（x1）=f（x2）（x1≠x2）时，x1+x2＜0．
17．已知i为虚数单位，则复数$Z=\frac{{1-\sqrt{3}i}}{{\sqrt{3}+i}}$的虚部为（　　）
A．1B．-1C．iD．-i
4．一个正三棱柱的主视图如图所示，则其左视图的面积（　　）
A．1B．2C．$\sqrt{3}$D．2$\sqrt{3}$
9．阅读程序框图（如图），如果输出的函数值在[1，3]上，则输入的实数x取值范围是（　　）
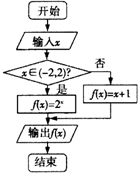
A．[0，log23]B．[-2，2]C．[0，log23]∪{2}D．[-2，log23]∪{2}
16．设x，y均为非零实数，且满足$\frac{xsin\frac{π}{5}+ycos\frac{π}{5}}{xcos\frac{π}{5}-ysin\frac{π}{5}}$=tan$\frac{9π}{20}$．
（1）求$\frac{y}{x}$的值；
（2）在△ABC中，若tanC=$\frac{y}{x}$，求sin2A+2cosB的最大值．
13．已知函数f（x）=ex，g（x）=-x2+ax-a（a∈R），点M，N分别在f（x），g（x）的图象上．
（1）若函数f（x）在x=0处的切线恰好与g（x）相切，求a的值；
（2）若点M，N的横坐标均为x，记h（x）=$\overrightarrow{OM}$•$\overrightarrow{ON}$，当x=0时，函数h（x）取得极大值，求a的范围．
14．在正方体中ABCD-A′B′C′D′中，点E为底面ABCD上的动点，若三棱锥B-D′EC的体积最大，则点E（　　）
A．位于线段AB上B．位于线段AD上C．只能在A点D．只能在AB的中点

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网