题目内容
1.近年来,某地区为促进本地区发展,通过不断整合地区资源、优化投资环境、提供投资政策扶持等措施,吸引外来投资,效果明显.该地区引进外来资金情况如表:| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 外来资金y(百亿元) | 5 | 6 | 7 | 8 | 10 |
(Ⅱ)根据所求回归直线方程预测该地区2017年(t=6)引进外来资金情况.
参考公式:回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$中斜率和截距的最小二乘估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$t.
分析 (Ⅰ)由题意求得$\sum_{i=1}^{n}$(ti-$\overline{t}$)(yi-$\overline{y}$)=4.4+1.2+0+0.8+5.6=12,$\sum_{i=1}^{n}$(ti-$\overline{t}$)2=10,利用最小二乘法求得线性回归方程的斜率和截距,即可求得y关于t的回归直线方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$;
(Ⅱ)当x=6时,代入线性回归方程,即可求得该地区2017年引进外来资金.
解答 解:(Ⅰ)由题意可知:
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| ti-$\overline{t}$ | -2 | -1 | 0 | 1 | 2 |
| (ti-$\overline{t}$)2 | 4 | 1 | 0 | 1 | 4 |
| 外来资金y(百亿元) | 5 | 6 | 7 | 8 | 10 |
| yi-$\overline{y}$ | -2.2 | -1.2 | -0.2 | 0.8 | 2.8 |
| (ti-$\overline{t}$)(yi-$\overline{y}$)= | 4.4 | 1.2 | 0 | 0.8 | 5.6 |
$\sum_{i=1}^{n}$(ti-$\overline{t}$)(yi-$\overline{y}$)=4.4+1.2+0+0.8+5.6=12,$\sum_{i=1}^{n}$(ti-$\overline{t}$)2=10,
∴$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{12}{10}$=1.2,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$t=7.2-1.2×3=3.6,
∴y关于t的回归方程为$\widehat{y}$=1.2t+3.6.…(8分)
(Ⅱ)当t=6时,$\widehat{y}$=1.2×6+3.6=10.8,
∴预测该地区2017年引进外来资金约10.8百亿元.…(12分)
点评 本题考查线性回归方程的应用,考查利用最小二乘法求线性回归方程的斜率和截距的方法,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
9.阅读程序框图(如图),如果输出的函数值在[1,3]上,则输入的实数x取值范围是( )
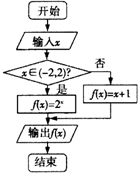

| A. | [0,log23] | B. | [-2,2] | C. | [0,log23]∪{2} | D. | [-2,log23]∪{2} |
6.某射击运动员进行打靶练习,已知打十枪每发的靶数为9,10,7,8,10,10,6,8,9,7,设其平均数为a,中位数为b,众数为c,则有( )
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |