题目内容
18.已知函数f(x)是R上的偶函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2-x,则f(2016)+f(-2017)的值为3.分析 根据题意可得函数的周期为4,然后根据函数的周期性,即可求解.
解答 解:∵f(x+2)=-f(x),
∴f(x+4)=f(x),
即函数f(x)是周期为4的周期函数,
∴f(-2017)=f(-504×4-1)=f(1),
f(2016)=f(504×4)=f(-3)=f(0),
当x∈[0,1]时,f(x)=2-x,
故f(1)=1,f(0)=2,
故f(2016)+f(-2017)=f(0)+f(1)=3,
故答案为:3.
点评 本题主要考查函数值的计算,利用条件求出函数的周期性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.如图,G是△ABC的重心,D为BC的中点,$\overrightarrow{AB}+\overrightarrow{AC}$=λ$\overrightarrow{GD}$,则λ的值为( )
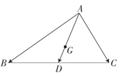

| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
6.在△ABC 中,∠A=60°,a=$\sqrt{13}$,b=4,则满足条件的△ABC ( )
| A. | 有两个 | B. | 有一个 | C. | 不存在 | D. | 有无数多个 |
13.设集合M={x|x2-3x-4<0},N={x|lgx<1},则M∩N=( )
| A. | (-1,4) | B. | (0,4) | C. | (0,10) | D. | (4,10) |
3.在△ABC中,A=60°,b=1,这个三角形的面积为$\sqrt{3}$,则sin C的值为( )
| A. | $\frac{{\sqrt{3}}}{8}$ | B. | $\frac{{\sqrt{15}}}{8}$ | C. | $\frac{{2\sqrt{39}}}{13}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
8.已知数列{an}满足2an+1-an=0,若a2=$\frac{1}{2}$,则数列{an}的前11项和为( )
| A. | 256 | B. | $\frac{1023}{4}$ | C. | $\frac{2047}{1024}$ | D. | $\frac{4095}{2048}$ |
