题目内容
6．在△ABC 中，∠A=60°，a=$\sqrt{13}$，b=4，则满足条件的△ABC （ ）| A． | 有两个 | B． | 有一个 | C． | 不存在 | D． | 有无数多个 |
分析 根据正弦定理结合三角形有解的条件进行判断即可．
解答 解：在△ABC中，∵∠A=60°，a=$\sqrt{13}$，b=4，
∴由正弦定理得 $\frac{a}{sinA}=\frac{b}{sinB}$，则sinB=$\frac{bsinA}{a}$=$\frac{2\sqrt{39}}{13}$，
∵b＞a，
∴B＞60°，
故B有一个为锐角，一个为钝角，满足条件的△ABC 有2个．
故选：A．
点评 本题主要考查三角形个数的判断及正弦定理在解三角形中的应用，属于基础题．
练习册系列答案
小学教材完全解读系列答案
相关题目
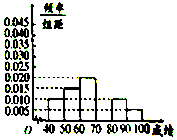如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩（均为整数）的频率分布直方图，该直方图恰好缺少了成绩在区间[70，80）内的图形，根据图形的信息，回答下列问题：
15．设函数f（x）是定义在R上的偶函数，f′（x）为其导函数．当x＞0时，xf′（x）+f（x）＞0，且f（1）=0，则不等式f（x）＞0的解集为（ ）
| A． | （-1，0）∪（0，1） | B． | （-1，0）∪（1，+∞） | C． | （-∞，-1）∪（1，+∞） | D． | （-∞，-1）∪（0，1） |