题目内容
12.已知函数f(x)=2x+2-x-4,则f(2)的值为$\frac{1}{4}$.分析 利用已知条件得到f(2)=22+2-2-4,由此能求出结果.
解答 解:∵函数f(x)=2x+2-x-4,
∴f(2)=22+2-2-4=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
2.函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则f(x)的解析式为( )
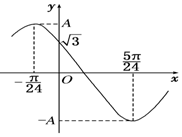

| A. | $y=2sin(4x+\frac{2π}{3})$ | B. | $y=4sin(2x+\frac{π}{3})$ | C. | $y=2\sqrt{3}sin(4x+\frac{π}{6})$ | D. | $y=-2sin(4x+\frac{2π}{3})$ |
20.已知命题p:“1,b,4”成等比数列”,命题q:“b=2”,那么p成立是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
7.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x+1},x≤0}\\{1-lo{g}_{2}x,x>0}\end{array}\right.$则f(f(4))=1.
17.设双曲线的虚轴长为2,焦距为$2\sqrt{3}$,则双曲线的渐近线方程为( )
| A. | $y=±\sqrt{2}x$ | B. | y=±2x | C. | $y=±\frac{{\sqrt{2}}}{2}x$或y=$±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
4.如图是用函数拟合解决实际问题的流程图,则矩形框中依次应填入( )
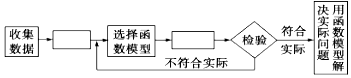

| A. | 整理数据、求函数关系式 | B. | 画散点图、进行模型修改 | ||
| C. | 画散点图、求函数关系式 | D. | 整理数据、进行模型修改 |