题目内容
2.已知向量$\overrightarrow{a}$=(x,y)(x,y∈R),$\overrightarrow{b}$=(1,2),若x2+y2=1,则|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值为$\sqrt{5}$-1.分析 利用|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(x-1)^{2}+(y-2)^{2}}$≥|$\overrightarrow{OP}$|-1,即可求出
解答 解:设O(0,0),P(1,2),
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(x-1)^{2}+(y-2)^{2}}$≥|$\overrightarrow{OP}$|-1=$\sqrt{{1}^{2}+{2}^{2}}$-1=$\sqrt{5}$-1,
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值为$\sqrt{5}$-1
点评 本题考查了向量的模的计算公式、点与圆的位置关系,考查了推理能力与计算能力,属于基础题

练习册系列答案
相关题目
7.已知平面向量$\overrightarrow a$与$\overrightarrow b$的夹角等于$\frac{π}{3}$,若|$\overrightarrow a$|=2,|$\overrightarrow b$|=3,则|2$\overrightarrow a$-3$\overrightarrow b$|=( )
| A. | $\sqrt{57}$ | B. | $\sqrt{61}$ | C. | 57 | D. | 61 |
14.如图所给的程序运行结果为S=41,那么判断框中应填入的关于k的条件是( )


| A. | k≥6 | B. | k≥5 | C. | k>6 | D. | k>5 |
11.椭圆的对称轴为坐标轴,若长、短轴之和为18,焦距为6,那么椭圆的方程为( )
| A. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
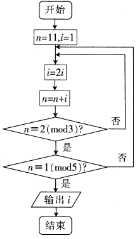 《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )
《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )