题目内容
2.函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则f(x)的解析式为( )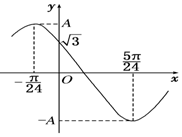
| A. | $y=2sin(4x+\frac{2π}{3})$ | B. | $y=4sin(2x+\frac{π}{3})$ | C. | $y=2\sqrt{3}sin(4x+\frac{π}{6})$ | D. | $y=-2sin(4x+\frac{2π}{3})$ |
分析 利用函数的周期求出ω,利用函数经过的特殊点求出A,利用函数的对称性求出φ,即可判断函数的解析式.
解答 解:由函数的图象可知:函数的周期为:2($\frac{5π}{24}+\frac{π}{24}$)=$\frac{π}{2}$,
可得:ω$\frac{2π}{\frac{π}{2}}$=4.
x=-$\frac{π}{24}$时,函数取得最大值,x=$\frac{5π}{24}$时,函数取得最小值,
可得:φ-$\frac{π}{6}$=$\frac{π}{2}$,φ+$\frac{5π}{6}$=$\frac{3π}{2}$,解得φ=$\frac{2π}{3}$,
x=0时,函数y=$\sqrt{3}$,可得A=2.
所以函数的解析式为:$y=2sin(4x+\frac{2π}{3})$.
故选:A.
点评 本题考查三角函数的解析式的求法,考查计算能力.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
12.对两个变量进行回归分析,则下列说法中不正确的是( )
| A. | 有样本数据得到的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$必经过样本中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越大,模型的拟合效果越好 | |
| C. | 用R2来刻画回归效果,R2越大,说明模型的拟合效果越好 | |
| D. | 若散点图中的样本呈条状分布,则变量y和x之间具有线性相关关系 |
13.已知集合A={-1,0,1,2},B={x|x(x-2)<0},则A∩B等于( )
| A. | {0} | B. | {-1} | C. | {1} | D. | {0,-1,1} |
10.已知函数$f(x)={cos^2}x+sinx,x∈[\frac{π}{3},\frac{5π}{6}]$,则f(x)的最大值与最小值的和为( )
| A. | $\frac{1}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{{2\sqrt{3}+5}}{4}$ | D. | $\frac{{2\sqrt{3}+6}}{4}$ |
7.某公司生产一种产品,固定成本为20 000元,每生产一单位的产品,成本增加100元,若总收入R与年产量x(0≤x≤390)的关系是$R(x)=-\frac{x^3}{9000}+400x,0≤x≤390$,则当总利润最大时,每年生产的产品单位数是( )
| A. | 300 | B. | 250 | C. | 200 | D. | 100 |
11.某几何体的三视图如图所示,则该几何体的体积为( )
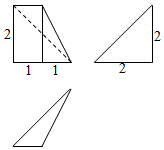

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
 阅读右边的程序框图,运行相应的程序,则输出的T值为39.
阅读右边的程序框图,运行相应的程序,则输出的T值为39.