题目内容
7．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x+1}，x≤0}\\{1-lo{g}_{2}x，x＞0}\end{array}\right.$则f（f（4））=1．分析 由已知得f（4）=1-log24=1-2=-1，从而f（f（4））=f（-1），由此能求出结果．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{{2}^{x+1}，x≤0}\\{1-lo{g}_{2}x，x＞0}\end{array}\right.$，
∴f（4）=1-log24=1-2=-1，
f（f（4））=f（-1）=2-1+1=20=1．
故答案为：1．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
15．若复数z=$\frac{3+i}{1+2i}$，则|z|=（ ）
| A． | $\frac{\sqrt{2}}{5}$ | B． | 2$\sqrt{2}$ | C． | $\sqrt{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
2．张家的3个鸡仔钻进了李家装有3个鸡仔的鸡笼里，现打开笼门，让鸡仔一个一个地走出来，若第一个走出来的是张家的鸡仔，那么第二个走出的也是张家的鸡仔的概率是（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{5}$ | D． | $\frac{3}{5}$ |
19．复数z=a+i（a∈R）的虚部为（ ）
| A． | 1 | B． | i | C． | -1 | D． | -i |
16．
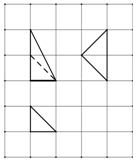某几何体的三视图如图所示，网格纸的小方格是边长为1的正方形，则该几何体中最长的棱长是（ ）
某几何体的三视图如图所示，网格纸的小方格是边长为1的正方形，则该几何体中最长的棱长是（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{6}$ | C． | $\sqrt{7}$ | D． | 3 |
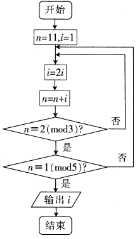《孙子算经》是中国公元四世纪的数学著作，其中接受了求解依次同余式的方法，他是数论中一个重要的定理，又称《中国剩余定理》，如图所示的程序框图的算法就是源于《中国剩余定理》，执行该程序框图，若正整数N除以正整数m后的余数为n，则记为N≡n（modm），例如11≡3（mod4），则输出的等于（ ）