题目内容
已知函数f(x)的定义域为(-1,1),求g(x)=f(a+x)+f(a-x)的定义域(-
<a<
).
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由函数的定义域列出不等式组,分别求出每个不等式的解集,根据a的范围比较出端点值的大小,求交集即得所求函数的定义域.
解答:
解:∵f(x)的定义域为(-1,1),
∴
,
解得
;
∵-
<a<
,
∴当
>a>0时,-1-a<-1+a<
<1-a<1+a,
∴不等式组的解为-1+a<x<1-a;
当a=0时,不等式组的解为-1<x<1;
当-
<a<0时,
>-a>0,∴-1+a<-1-a<-
<1+a<1-a,
∴不等式组的解为-1-a<x<1+a;
综上,
>a≥0时,函数的定义域是(-1+a,1-a),
-
<a<0时,函数的定义域是(-1-a,1+a).
∴
|
解得
|
∵-
| 1 |
| 2 |
| 1 |
| 2 |
∴当
| 1 |
| 2 |
| 1 |
| 2 |
∴不等式组的解为-1+a<x<1-a;
当a=0时,不等式组的解为-1<x<1;
当-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴不等式组的解为-1-a<x<1+a;
综上,
| 1 |
| 2 |
-
| 1 |
| 2 |
点评:本题考查了复合函数的定义域的求法问题,解题时应根据已知函数的定义域列出不等式组,求每个不等式解集的交集,要讨论端点处值的大小,是易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
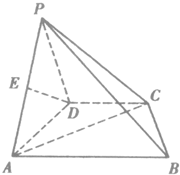 如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.