题目内容
已知等差数列{an}满足:a3=7,a5+a7=26,数列{an}的前n项和为Sn.
(Ⅰ)求an及Sn;
(Ⅱ)令bn=
(n∈N*),求数列{bn}的前n项和.
(Ⅰ)求an及Sn;
(Ⅱ)令bn=
| 8 | ||
|
考点:等差数列的性质,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)设等差数列{an}的公差为d,根据等差数列的通项公式和题意列出方程,求出首项、公差,代入等差数列的通项公式、前n项和公式,求出an及Sn;
(Ⅱ)由(Ⅰ)和题意求出bn,利用裂项相消法求出数列{bn}的前n项和.
(Ⅱ)由(Ⅰ)和题意求出bn,利用裂项相消法求出数列{bn}的前n项和.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,
因为a3=7,a5+a7=26,所以
,解得
,
所以an=3+2(n-1)=2n+1;
Sn=3n+
×2=n2+2n;
(Ⅱ)由(Ⅰ)知an=2n+1,所以bn=
=
=
=2(
-
),
所以数列{bn}的前n项和Tn=2[(1-
)+(
-
)+…+(
-
)]
=2(1-
)=
,
即数列{bn}的前n项和是
.
因为a3=7,a5+a7=26,所以
|
|
所以an=3+2(n-1)=2n+1;
Sn=3n+
| n(n-1) |
| 2 |
(Ⅱ)由(Ⅰ)知an=2n+1,所以bn=
| 8 | ||
|
| 8 |
| (2n+1)2-1 |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
所以数列{bn}的前n项和Tn=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=2(1-
| 1 |
| n+1 |
| 2n |
| n+1 |
即数列{bn}的前n项和是
| 2n |
| n+1 |
点评:本题考查等差数列的通项公式、前n项和公式,裂项相消法求数列的前n项和,以及方程思想,属于中档题.

练习册系列答案
相关题目
定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b),满足f′(x1)=
,f′(x2)=
,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=
x3-x2+a是[0,a]上“双中值函数”,则实数a的取值范围是( )
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
| 1 |
| 3 |
| A、(1,3) | ||||
B、(
| ||||
C、(1,
| ||||
D、(1,
|
在等差数列{an}中,若a3=2,a5=8,则S7等于( )
| A、16 | B、18 | C、35 | D、22 |
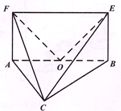 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
 如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=
如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=