题目内容
5.已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的上、下顶点分别为M,N点,P在椭圆C外,直线PM交椭圆于点A,若PN⊥NA,则点P的轨迹方程是( )| A. | y=x2+1(x≠0) | B. | y=x2+3(x≠0) | ||
| C. | y2-$\frac{{x}^{2}}{2}$=1(y>0,x≠0) | D. | y=3(x≠0) |
分析 根据向量数量积的坐标运算,求得xx0+(y0+1)(y+1)=0,根据直线斜率公式,由A在椭圆方程,代入即可求得P的轨迹方程.
解答 解:由题意可知设P(x,y),(x≠0),由椭圆方程椭圆C:$\frac{{x}^{2}}{2}$+y2=1,A(x0,y0),M(0,1),N(0,-1),
由PN⊥NA,$\overrightarrow{NA}$•$\overrightarrow{NP}$=0,即(x0,y0+1)(x,y+1)=0,则xx0+(y0+1)(y+1)=0,①
由直线P,C,A三点共线,$\frac{y-1}{x}$=$\frac{{y}_{0}-1}{{x}_{0}}$,x=$\frac{{x}_{0}(y-1)}{{y}_{0}-1}$,②
代入将②代入①,x02(y-1)+(y02-1)(y+1)=0,
由A在椭圆上,则y02=1-$\frac{{x}_{0}^{2}}{2}$,
代入整理得:y=3(x≠0),
点P的轨迹方程y=3(x≠0),
故选:D.
点评 本题考查椭圆的标准方程及性质,轨迹方程的求法,向量的坐标运算,考查计算能力,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
16.已知y=8x2,则它的焦点坐标为( )
| A. | (2,0) | B. | (0,2) | C. | $({\frac{1}{32},0})$ | D. | $({0,\frac{1}{32}})$ |
20.已知数列{an}等差数列,a10=10,其前10项和S10=60,则其公差d=( )
| A. | -$\frac{2}{9}$ | B. | $\frac{2}{9}$ | C. | -$\frac{8}{9}$ | D. | $\frac{8}{9}$ |
17.已知数列{an}是等差数列a10=10,其前10项和S10=55,则其公差d=( )
| A. | 0 | B. | 1 | C. | C-1 | D. | $\frac{9}{10}$ |
14.盒中装有形状,大小完全相同的5个小球,其中红色球3个,黄色球2个,若从中随机取出2个球,则所取出的2个球颜色不同的概率等于( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |

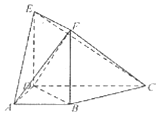 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,