题目内容
13.己知△ABC中,AB=2,AC=$\sqrt{3}$BC,则△ABC面积的最大值是$\sqrt{3}$.分析 设BC=x,则△ABC面积 S=$\frac{1}{2}AB•BCsinB=xsinB$=$\sqrt{{x}^{2}(1-co{s}^{2}B)}$又cosB=$\frac{B{C}^{2}+A{B}^{2}=A{C}^{2}}{2BC}=\frac{2-B{C}^{2}}{2BC}=\frac{2-{x}^{2}}{x}$.
即S=$\frac{1}{2}\sqrt{-{x}^{4}+8{x}^{2}-4}=\frac{1}{2}\sqrt{-({x}^{2}-4)^{2}+12}$即可求出最值.
解答 解:设BC=x,则△ABC面积 S=$\frac{1}{2}AB•BCsinB=xsinB$=$\sqrt{{x}^{2}(1-co{s}^{2}B)}$
又因为cosB=$\frac{B{C}^{2}+A{B}^{2}=A{C}^{2}}{2BC}=\frac{2-B{C}^{2}}{2BC}=\frac{2-{x}^{2}}{x}$.
即S=$\frac{1}{2}\sqrt{-{x}^{4}+8{x}^{2}-4}=\frac{1}{2}\sqrt{-({x}^{2}-4)^{2}+12}$≤$\sqrt{3}$
故答案为:$\sqrt{3}$
点评 本题主要考查了余弦定理和面积公式在解三角形中的应用.当涉及最值问题时,可考虑用函数的单调性和定义域等问题.属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
8.己知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1(a>0)的一个焦点与抛物线y2=8x的焦点重合,则a=( )
| A. | $\sqrt{19}$ | B. | $\sqrt{13}$ | C. | 2 | D. | 1 |
5.已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的上、下顶点分别为M,N点,P在椭圆C外,直线PM交椭圆于点A,若PN⊥NA,则点P的轨迹方程是( )
| A. | y=x2+1(x≠0) | B. | y=x2+3(x≠0) | ||
| C. | y2-$\frac{{x}^{2}}{2}$=1(y>0,x≠0) | D. | y=3(x≠0) |
2.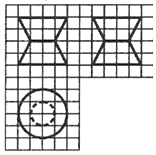 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )
 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |