题目内容
16．已知y=8x2，则它的焦点坐标为（ ）| A． | （2，0） | B． | （0，2） | C． | $（{\frac{1}{32}，0}）$ | D． | $（{0，\frac{1}{32}}）$ |
分析 根据题意，先将抛物线的方程变形可得标准方程，分析可得其焦点位置以及p的值，由焦点坐标公式计算可得答案．
解答 解：根据题意，抛物线的方程为y=8x2，
则标准方程为x2=$\frac{1}{8}$y，
其焦点在y轴正半轴上，且p=$\frac{1}{16}$，
则其焦点坐标为（0，$\frac{1}{32}$）；
故选：D．
点评 本题考查抛物线的标准方程，注意先将其方程变为标准方程．
练习册系列答案
相关题目
11．数列{an}满足a1=2，an+1=$\frac{1}{{1-{a_n}}}（n∈{N^+}）$，则a2017=（ ）
| A． | -2 | B． | -1 | C． | 2 | D． | $\frac{1}{2}$ |
8．己知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1（a＞0）的一个焦点与抛物线y2=8x的焦点重合，则a=（ ）
| A． | $\sqrt{19}$ | B． | $\sqrt{13}$ | C． | 2 | D． | 1 |
5．已知椭圆C：$\frac{{x}^{2}}{2}$+y2=1的上、下顶点分别为M，N点，P在椭圆C外，直线PM交椭圆于点A，若PN⊥NA，则点P的轨迹方程是（ ）
| A． | y=x2+1（x≠0） | B． | y=x2+3（x≠0） | ||
| C． | y2-$\frac{{x}^{2}}{2}$=1（y＞0，x≠0） | D． | y=3（x≠0） |
6．某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x的值（ ）
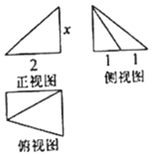
| A． | 2 | B． | 3 | C． | $\frac{3}{2}$ | D． | $\frac{9}{2}$ |