题目内容
5.已知命题 p:?x0∈R,x2-3x+3≤0,则¬p 为真命题(填“真”或“假”).分析 利用特称命题的否定是全称命题,写出结果即可.
解答 解:因为特称命题的否定是全称命题,
所以命题 p:?x0∈R,x2-3x+3≤0,则¬p 为:?x∈R,x2-3x+3>0,
因为:x2-3x+3=(x-$\frac{3}{2}$)2+$\frac{3}{4}$>0,所以命题是真命题.
故答案为:真.
点评 本题考查命题的真假判断与应用,命题的否定形式,是基础题.

练习册系列答案
相关题目
16.甲、乙、丙、丁4人站成一排,要求甲、乙相邻,则不同的排法数是( )
| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
13.已知直线l:x-y+a=0,点A(-2,0),B(2,0).若直线l上存在点P满足AB⊥BP,则实数a的取值范围为( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [0,2$\sqrt{2}$] | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-2,2] |
12.已知a,b∈R,则“a>0”是“a+b2>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 是函数
是函数 定义域内的一个区间,若存在
定义域内的一个区间,若存在 ,使得
,使得 ,则称
,则称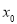 是
是 的一个“次不动点”,也称
的一个“次不动点”,也称 在区间
在区间 上存在次不动点.若函数
上存在次不动点.若函数 在区间
在区间 上存在次不动点,则实数
上存在次不动点,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 已知定义域为R的函数f(x),若函数y=$\frac{f′(x)}{x}$的图象如图所示,给出下列命题:
已知定义域为R的函数f(x),若函数y=$\frac{f′(x)}{x}$的图象如图所示,给出下列命题: 是函数
是函数 定义域内的一个区间,若存在
定义域内的一个区间,若存在 ,使得
,使得 ,则称
,则称 是
是 的一个“次不动点”,也称
的一个“次不动点”,也称 在区间
在区间 上存在次不动点.若函数
上存在次不动点.若函数 在区间
在区间 上存在次不动点,则实数
上存在次不动点,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.