题目内容
13.已知直线l:x-y+a=0,点A(-2,0),B(2,0).若直线l上存在点P满足AB⊥BP,则实数a的取值范围为( )| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [0,2$\sqrt{2}$] | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-2,2] |
分析 问题转化为求直线l与圆x2+y2=22有公共点时,a的取值范围,利用数形结合思想能求出结果.
解答 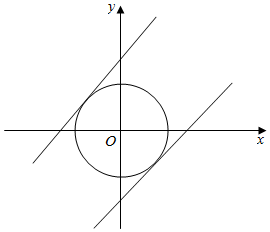 解:∵直线l:x-y+a=0,点A(-2,0),B(2,0),
解:∵直线l:x-y+a=0,点A(-2,0),B(2,0),
直线l上存在点P满足AB⊥BP,
∴如图,直线l与圆x2+y2=22有公共点,
∴圆心O(0,0)到直线l:x-y+a=0的距离:
d=$\frac{|a|}{\sqrt{2}}$≤2,
解得$-2\sqrt{2}≤a≤2\sqrt{2}$.
∴实数a的取值范围为[-2$\sqrt{2}$,2$\sqrt{2}$].
故选:C.
点评 本题考查实数的取值范围的求法,考查直线方程、圆、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知点A(-1,0),B(1,0),若圆x2+y2-8x-6y+25-m=0上存在点P使$\overrightarrow{PA}•\overrightarrow{PB}=0$,则m的最小值为16.
4.函数f(x)=lnx的切线方程为y=kx,则实数k=( )
| A. | $\frac{1}{e}$ | B. | 1 | C. | e | D. | e2 |
1.在6件产品中有4件合格品,2件次品,产品检验时,从中抽取3件,至少有1件次品的抽法有( )
| A. | 10 | B. | 16 | C. | 32 | D. | 24 |
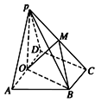 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$. .
. 时,求不等式
时,求不等式 的解集;
的解集; 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.