题目内容
16. 已知定义域为R的函数f(x),若函数y=$\frac{f′(x)}{x}$的图象如图所示,给出下列命题:
已知定义域为R的函数f(x),若函数y=$\frac{f′(x)}{x}$的图象如图所示,给出下列命题:①f′(1)=f′(-1)=0;
②函数f(x)在区间(-∞,-1)上单调递增;
③当x=1时,函数f(x)取得极小值;
④方程xf′(x)=0与f(x)=0均有三个实数根.
其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用导函数的符号以及导函数值,判断函数的单调性与极值点,判断零点个数推出结果即可.
解答 解:由题意可知:①f′(1)=f′(-1)=0;正确;
②函数f(x)在区间(-∞,-1)上f′(x)>0,所以函数是单调递增;正确;
③x∈(0,1)时f′(x)<0,函数是减函数,x∈(1,+∞)上f′(x)>0,函数是增函数,
当x=1时,函数f(x)取得极小值;正确;
④方程f(x)=0可能没有实数根.如图:
所以方程xf′(x)=0与f(x)=0均有三个实数根.不正确;
故选:C.
点评 本题考查命题真假的判断,函数的导数的应用,函数的单调性以及图象的应用,是中档题.

练习册系列答案
相关题目
7.令(3-2x)n=a0+a1x+a2x2+…anxn,n∈N*,且a1+a2+…+an=-242,则a3=( )
| A. | -3240 | B. | -1080 | C. | -720 | D. | -96 |
1.用数学归纳法证明“1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$<n(n≥2)”时,由n=k的假设证明n=k+1时,不等式左边需增加的项数为( )
| A. | 2k-1 | B. | 2k-1 | C. | 2k | D. | 2k+1 |
7.已知空间两条不同的直线m,n和两个不同的平面α,β,以下能推出“α⊥β”的是( )
| A. | m⊥n,m∥α,n∥β | B. | m∥n,m⊥α,n⊥β | C. | m⊥n,m⊥α,α∩β=n | D. | m∥n,m⊥α,n?β |
 .
. 时,求函数
时,求函数 在
在 上的最小值和最大值;
上的最小值和最大值; 时,讨论函数
时,讨论函数 的单调性;
的单调性; ,对任意的
,对任意的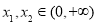 ,且
,且 ,都有
,都有 恒成立,若存在,求出
恒成立,若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.