题目内容
函数f(x)=
是奇函数,且f(1)=3.
(1)求实数a,b的值.
(2)用定义法证明f(x)在(0,
]上是减函数;
(3)求f(x)在(0,+∞)的值域.
| ax2+2 |
| x+b |
(1)求实数a,b的值.
(2)用定义法证明f(x)在(0,
| 2 |
(3)求f(x)在(0,+∞)的值域.
考点:函数奇偶性的性质,函数的值域
专题:函数的性质及应用
分析:(1)由于函数f(x)=
是奇函数,且f(1)=3.可得f(-1)=
=-3,f(1)=
=3.解出即可.
(2)利用减函数的定义即可证明;
(3)利用基本不等式即可得出.
| ax2+2 |
| x+b |
| a+2 |
| -1+b |
| a+2 |
| 1+b |
(2)利用减函数的定义即可证明;
(3)利用基本不等式即可得出.
解答:
(1)解:∵函数f(x)=
是奇函数,且f(1)=3.
∴f(-1)=
=-3,f(1)=
=3.
解得a=1,b=0.
∴f(x)=
=x+
.
(2)证明:?0<x1<x2≤
,
则x1-x2<0,0<x1x2<2,即x1x2-2<0.
∴f(x1)-f(x2)=x1+
-(x2+
)=
>0.
∴f(x1)>f(x2).
∴f(x)在(0,
]上是减函数.
(3)∵x∈(0,+∞),
∴f(x)≥2
=2
,当且仅当x=
时取等号.
∴f(x)在(0,+∞)的值域是[2
,+∞).
| ax2+2 |
| x+b |
∴f(-1)=
| a+2 |
| -1+b |
| a+2 |
| 1+b |
解得a=1,b=0.
∴f(x)=
| x2+2 |
| x |
| 2 |
| x |
(2)证明:?0<x1<x2≤
| 2 |
则x1-x2<0,0<x1x2<2,即x1x2-2<0.
∴f(x1)-f(x2)=x1+
| 2 |
| x1 |
| 2 |
| x2 |
| (x1-x2)(x1x2-2) |
| x1x2 |
∴f(x1)>f(x2).
∴f(x)在(0,
| 2 |
(3)∵x∈(0,+∞),
∴f(x)≥2
x•
|
| 2 |
| 2 |
∴f(x)在(0,+∞)的值域是[2
| 2 |
点评:本题考查了函数的奇偶性与单调性、值域、基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
f(x)的定义域为R,f(2+x)=f(2-x),-1<x<2时,f(x)=(
)x,则有( )
| 1 |
| 2 |
A、f(-
| ||
B、f(4)<f(1)<f(-
| ||
C、f(1)<f(-
| ||
D、f(1)<f(4)<f(-
|
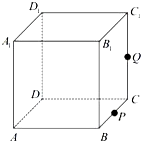 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是