题目内容
15.若椭圆的中心为坐标原点,长轴长为4,一条准线方程为x=-4,则该椭圆被直线y=x+1截得的弦长为$\frac{24}{7}$.分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意,利用椭圆性质求出椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,由此能求出该椭圆被直线y=x+1截得的弦长.
解答 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意,椭圆的焦点在x轴上,且2a=4,$\frac{{a}^{2}}{c}$=4,
解得a=2,c=1,∴b2=a2-c2=3,
∴椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=x+1}\end{array}\right.$,得7x2+8x-8=0,
设直线y=x+1与椭圆交于A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{8}{7}$,x1x2=-$\frac{8}{7}$,
∴该椭圆被直线y=x+1截得的弦长为:
|AB|=$\sqrt{2[(-\frac{8}{7})^{2}+4×\frac{8}{7}]}$=$\frac{24}{7}$.
故答案为:$\frac{24}{7}$.
点评 本题考查椭圆弦长的求法,是中档题,解题时要认真审题,注意椭圆的简单性质和椭圆弦长公式的合理运用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
4.设经过椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上的任意两点的连线(该连线不与x轴垂直)的垂直平分线与x轴交点的横坐标为x0,则x0的取值范围是( )
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-1,1] | D. | (-1,1) |
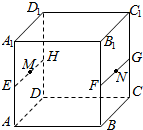 若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )
若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )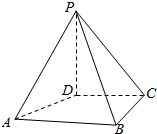 如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.