题目内容
14.三角函数y=sin($\frac{π}{6}$-2x)+cos2x的振幅和最小正周期分别为( )| A. | $\sqrt{3}$,$\frac{π}{2}$ | B. | $\sqrt{3}$,π | C. | $\sqrt{2}$,$\frac{π}{2}$ | D. | $\sqrt{2}$,π |
分析 直接利用特殊角的三角函数值以及两角和的正弦函数公式、余弦函数公式化简函数解析式为y=$\sqrt{3}$cos(2x+$\frac{π}{6}$),然后求解最小正周期和振幅.
解答 解:∵y=sin($\frac{π}{6}$-2x)+cos2x
=$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x+cos2x
=$\frac{3}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x
=$\sqrt{3}$cos(2x+$\frac{π}{6}$),
∴三角函数y=sin($\frac{π}{6}$-2x)+cos2x的振幅和最小正周期分别为:$\sqrt{3}$,π.
故选:B.
点评 本题主要考查了三角函数的化简,两角和与差的三角函数,三角函数周期的求法,属于基本知识的考查.

练习册系列答案
相关题目
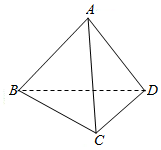 在空间四边形ABCD中,AB=AC=AD=1
在空间四边形ABCD中,AB=AC=AD=1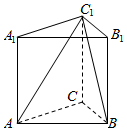 如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.
如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.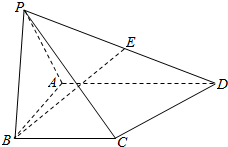 如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点.
如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点.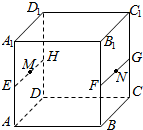 若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )
若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )