题目内容
7.函数f(x)=2cos(4x+$\frac{π}{3}$)-1的最小正周期为$\frac{π}{2}$,f($\frac{π}{3}$)=0.分析 根据周期的定义和函数的值的求法即可求出.
解答 解:函数f(x)=2cos(4x+$\frac{π}{3}$)-1的最小正周期T=$\frac{2π}{4}$=$\frac{π}{2}$,
f($\frac{π}{3}$)=2cos(4×$\frac{π}{3}$+$\frac{π}{3}$)-1=2cos$\frac{π}{3}$-1=0,
故答案为:$\frac{π}{2}$,0.
点评 本题考查了余弦函数的最小正周期的和函数值的求法,属于基础题.

练习册系列答案
相关题目
17.若|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,则|2$\overrightarrow{a}$$-\overrightarrow{b}$|=( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 0 | D. | $\sqrt{2}$ |
15.化简sin2β+cos4β+sin2βcos2β的结果是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
 △ABC中,AB=5,AC=12,BC=13,P为△ABC平面外一点,PA=PB=PC=7
△ABC中,AB=5,AC=12,BC=13,P为△ABC平面外一点,PA=PB=PC=7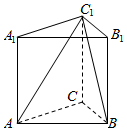 如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.
如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.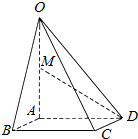 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.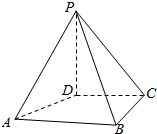 如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.