题目内容
已知过定点P（2，0）的直线l与曲线y=
相交于A，B两点，O为坐标原点，当S△AOB=1时，直线l的倾斜角为（ ）
| 2-x2 |
| A、150° | B、135° |
| C、120° | D、不存在 |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：判断曲线的形状，利用三角形的面积求出∠AOB，推出原点到直线的距离，建立方程求出直线的斜率，然后求解倾斜角．
解答：
解：曲线y=
，表示的图形是以原点为圆心半径为
的上半个圆，
过定点P（2，0）的直线l设为：y=k（x-2）．（k＜0）即kx-y-2k=0．
S△AOB=1．
∴
×
×
sin∠AOB=1，
可得∠AOB=90°，
三角形AOB是等腰直角三角形，原点到直线的距离为：1．
∴1=
，
解得k=±
，∵k＜0．∴k=-
，
∴直线的倾斜角为150°．
故选：A．
| 2-x2 |
| 2 |
过定点P（2，0）的直线l设为：y=k（x-2）．（k＜0）即kx-y-2k=0．
S△AOB=1．
∴
| 1 |
| 2 |
| 2 |
| 2 |
可得∠AOB=90°，
三角形AOB是等腰直角三角形，原点到直线的距离为：1．
∴1=
| |2k| | ||
|
解得k=±
| ||
| 3 |
| ||
| 3 |
∴直线的倾斜角为150°．
故选：A．
点评：本题考查直线与曲线的位置关系的应用，点到直线的距离公式，考查转化思想以及计算能力．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
相关题目
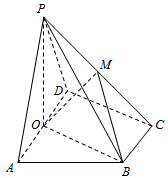在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=
在如图所示的几何体中，四边形ABCD和ABEF均为矩形，M为AF的中点，BN⊥CE与N．