题目内容
若定义在R上的偶函数f(x)满足f(x+1)=-f(x),并且当x∈[0,1]时,f(x)=2x-1,则函数y=f(x)-log3|x|的零点个数是 .
考点:函数零点的判定定理,函数奇偶性的性质
专题:
分析:在同一个坐标系中画出函数y=f(x)的图象与函数y=log3|x|的图象,这两个函数图象的交点个数即为所求.
解答:
解:∵定义在R上的偶函数f(x)满足f(x+1)=-f(x),
∴满足f(x+2)=f(x),
故函数的周期为2.
当x∈[0,1]时,f(x)=2x-1,
故当x∈[-1,0]时,f(x)=-2x-1.
函数y=f(x)-log3|x|的零点的个数等于函数y=f(x)的图象与函数y=log3|x|的图象的交点个数.
在同一个坐标系中画出函数y=f(x)的图象与函数y=log3|x|的图象,如图所示:
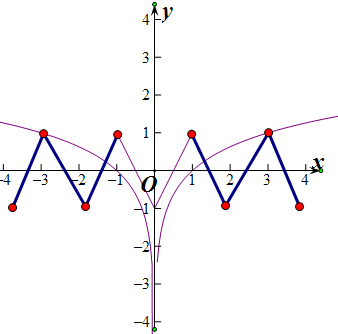
显然函数y=f(x)的图象与函数y=log3|x|的图象有4个交点,
故答案为:4.
∴满足f(x+2)=f(x),
故函数的周期为2.
当x∈[0,1]时,f(x)=2x-1,
故当x∈[-1,0]时,f(x)=-2x-1.
函数y=f(x)-log3|x|的零点的个数等于函数y=f(x)的图象与函数y=log3|x|的图象的交点个数.
在同一个坐标系中画出函数y=f(x)的图象与函数y=log3|x|的图象,如图所示:

显然函数y=f(x)的图象与函数y=log3|x|的图象有4个交点,
故答案为:4.
点评:本题考查了根的存在性及根的个数判断,以及函数与方程的思想,解答关键是运用数形结合的思想,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
在正方体ABCD-A1B1C1D1中,动点P在底面ABCD内,且P到棱AD的距离与到面对角线BC1的距离相等,则点P的轨迹是( )
| A、线段 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
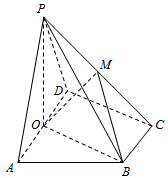 在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
 在如图所示的几何体中,四边形ABCD和ABEF均为矩形,M为AF的中点,BN⊥CE与N.
在如图所示的几何体中,四边形ABCD和ABEF均为矩形,M为AF的中点,BN⊥CE与N.