题目内容
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取15名路人进行了问卷调查,得到了如下列联表:
已知在这15人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料判断是否能在犯错误的概率不超过0.05的前提下认为反感“中国式过马路”与性别有关?
(2)若从这些不反感的人中随机抽取4人,要求女性人数不少于男性人数,并设女性人数为随机变量ξ,求ξ的所有取值和相应的概率.
附:K2=
,其中 n=a+b+c+d
| 男性 | 女性 | 合计 | |
| 反感 | 5 | ||
| 不反感 | 4 | ||
| 合计 | 15 |
| 8 |
| 15 |
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料判断是否能在犯错误的概率不超过0.05的前提下认为反感“中国式过马路”与性别有关?
(2)若从这些不反感的人中随机抽取4人,要求女性人数不少于男性人数,并设女性人数为随机变量ξ,求ξ的所有取值和相应的概率.
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| p(K2,k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)在这15人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
,进而做出男生的人数,填好表格.再根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出能在犯错误的概率不超过0.05的前提下认为反感“中国式过马路”与性别有关;
(2)随机变量ξ的所有取值为2,3,4,利用组合知识,分别计算出它们的概率.
| 8 |
| 15 |
(2)随机变量ξ的所有取值为2,3,4,利用组合知识,分别计算出它们的概率.
解答:
解:(1)依题意,反感“中国式过马路”的路人共8人,故列联表如下:
…(3分)
设H0:“中国式过马路”与性别无关.
由已知数据得K2=
≈0.579<3.841
所以在犯错误的概率不超过0.05的前提下没有充分的证据认为反感“中国式过马路”与性别有关.…(6分)
(2)依题意,随机变量ξ的所有取值为2,3,4.…(7分)
它们对应的概率分别为:P(ξ=2)=
=
,P(ξ=3)=
=
,P(ξ=4)=
=
.…(13分)
| 男性 | 女性 | 合计 | |
| 反感 | 5 | 3 | 8 |
| 不反感 | 3 | 4 | 7 |
| 合计 | 8 | 7 | 15 |
设H0:“中国式过马路”与性别无关.
由已知数据得K2=
| 15×(5×4-3×3)2 |
| 8×7×8×7 |
所以在犯错误的概率不超过0.05的前提下没有充分的证据认为反感“中国式过马路”与性别有关.…(6分)
(2)依题意,随机变量ξ的所有取值为2,3,4.…(7分)
它们对应的概率分别为:P(ξ=2)=
| ||||
|
| 18 |
| 35 |
| ||||
|
| 12 |
| 35 |
| ||
|
| 1 |
| 35 |
点评:本题考查了独立性检验、古典概型的概率计算,考查了组合数公式的应用,解题的关键是求得符合条件的基本事件个数.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
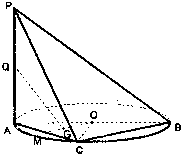 如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆0上异于A,B的点,
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆0上异于A,B的点,